作者別: Satoshi Morita

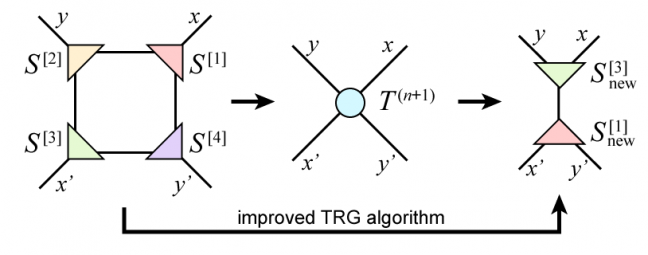
テンソルネットワーク法は，多体問題のための強力な数値計算手法として研究開発が進められている．テンソルくりこみ群 (Tensor Renormalization Group, TRG) [1] に代表される実空間のくりこみの方法は，粗視化によりテンソルネットワークの縮約を効率良く計算する近似手法である．テンソルの次元（ボンド次元）を大きくすることで近似の精度が向上する．しかしながら，TRGでは計算コストはボンド次元の6乗に比例して増大する．そのため，計算精度を損なわず計算量を削減する手法の開発が求められている．

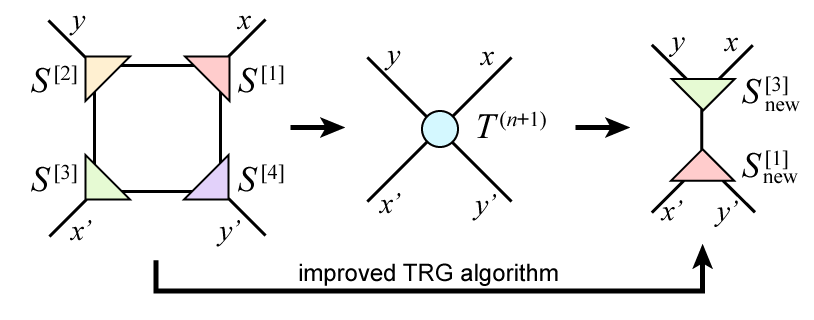
本研究で我々は，乱択アルゴリズムによる特異値分解 (RSVD) [2] を用いたTRGの新しいアルゴリズムを提案し，TRGの計算コストをボンド次元の5乗に削減することに成功した [3]．TRGの主要な演算は「分解」と「縮約」であるが，どちらも計算量がボンド次元の6乗に比例する．RSVDによる分解の計算量削減だけでなく，4階のテンソルを明示的に生成しないことで縮約の計算量も同時に削減する点が提案手法の肝となっている．RSVDは乱数を用いるため統計誤差が含まれるが，オーバーサンプリング変数を増やすことで誤差を減らすことができる．我々は2次元Ising模型におけるベンチマークにより，オーバーサンプリング変数がボンド次元と同じ程度であれば全特異値を求める場合と同じ精度で自由エネルギーが計算できることを示した．

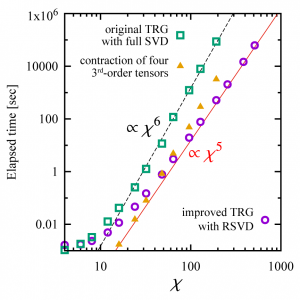
他のテンソルネットワーク法でも主要な演算は，TRGと同じく「分解」と「縮約」である．そのため，乱択アルゴリズムを用いた手法は，数多くのテンソルネットワーク法に応用されることが期待される．

References

1. M. Levin and C. P. Nave, Phys. Rev. Lett. 99, 120601 (2007).
2. N. Halko, P. G. Martinsson, and J. A. Tropp, SIAM Rev. 53, 217 (2011).
3. S. Morita, R. Igarashi, H.-H. Zhao, and N. Kawashima, Phys. Rev. E 97, 033310 (2018).

相互作用が確率的に分布したスピングラス模型は，1975年に提案された Edwards-Anderson 模型を起源とし，ランダムネスとフラストレーションが磁気構造に与える影響について古くから盛んに研究されている．現在では，2次元ランダムボンドイジング模型の相転移点が Kitaev による量子トーラス符号の誤り訂正限界とも関連付けられるなど，統計力学以外の分野からも興味が持たれている．スピンの向きに対する熱平均と相互作用の強さに対する配位平均の2重の平均操作があるため，解析的な計算は困難であり，一般のランダムボンドイジング模型の厳密解は知られていない．一方，McCoy-Wu 模型や Shankar-Murthy 模型など正方格子上で層状に乱れた相互作用を持つイジング模型では，並進対称性より転送行列が簡単に表現できるため厳密解を導出することができる．我々は Shankar-Murthy 模型を拡張した2次元層状ランダムイジング模型を考察し，絶対零度における相転移点を厳密に導出することに成功した．これはランダムボンドイジング模型における非自明な絶対零度相転移点を解析的に導出した初めての例となっている．

我々が考察した模型は，図1bのように水平方向に2つずらすと元にもどる並進対称性を持っており，水平方向の相互作用のみランダムで垂直方向は強磁性相互作用になっている．この模型は，周期が1の場合に相当する Shankar-Murthy 模型 (図1a) の自明な拡張となっている．垂直方向に進むの転送行列を並進対称性によりブロック対角化し，絶対零度におけるリヤプノフ指数と1次元ランダム磁場イジング模型の基底エネルギーの対応関係に着目することで，リヤプノフ指数の最大値を与えるブロックが変わる点として相転移点を導出した．確率 \(p\) で強磁性相互作用，確率 \(1−p\) で反強磁性相互作用をとる確率分布の場合，得られた強磁性相と常磁性相の絶対零度相転移確率は，正方格子と六角格子 (図1c) でそれぞれ
$$p_c^{(\text{SQ})}=\frac{\sqrt{5}−1}{2}=0.6180⋯$$
$$p_c^{(\text{HEX})}=1−2\sin\frac{\pi}{18}=0.6527⋯$$
である．

また，有限温度におけるリヤプノフ指数は，指数関数よりも早く収束するBaiの手法等を用いて数値計算することが可能である．これらの手法を用いて有限温度におけるリヤプノフ指数の交点を計算し，全領域の確率-温度相図 (図2) を高精度に決定した．

[参考文献]

[1] R. Shankar and G. Murthy: Phys. Rev. B 36, 536 (1987).
[2] S. Morita and S. Suzuki: J. Stat. Phys. 162, 123 (2016).

(by 森田 悟史)

連続相転移で現れる臨界現象では，通常，「イレレバント」な性質は大きな役割を果たさずに「レレバント」な性質により臨界指数などの特徴が支配される．そのため，臨界現象は物理系の詳細に依存せずに，物理系の対称性や空間の次元等の少数の性質だけで，その振る舞いの特徴が決まっている．しかし，特殊な場合には，臨界現象に重要な役割を果たすイレレバント変数が存在し，それは「危険なイレレバント場」と呼ばれている．我々は，そのような危険なイレレバント変数が物理系の対称性を低下させる場合について考察し，臨界現象を特徴付ける臨界指数の間に新しいスケーリング関係式が成立することを示した．

我々は図1のような二つの固定点（臨界点を支配する臨界固定点 \(X\) と，秩序状態を支配する固定点 \(Y\)）を含む一般的なくり込み群の流れを考察した．このくり込みの流れでは，対称性を破る場 \(\lambda\) は，臨界点近傍では，ある長さスケール \(\xi\) まででほとんどゼロになる一方で，もう少し長いスケール \(\xi^\prime\) では，その値が有限に「復活」する．そのため，二つの長さスケールの中間の大きさ， \(\xi \ll L \ll \xi^\prime\) では， 対称性を破る場 \(\lambda\) があたかも無い（\(\lambda=0\)）ように感じられ，新しい対称性が現れたように見えることになる．

このようなくり込みの流れが実現している古典的な例は，３次元のq状態クロック模型と呼ばれる，q 個の向やすい方向を持った，平面内で自由な方向を向けるベクトルスピンが相互作用する模型である．この模型において，短い相関長 \(\xi\) を特徴付ける臨界指数 \(\nu\) と長い相関長 \(\xi^\prime\) を特徴付ける臨界指数 \(\nu^\prime\) との間に成立するスケーリング関係式については，これまでにドメインウォールの存在を仮定し，その自由エネルギーが系の体積や断面積に比例するすると考える議論が行われていた[2,3,4]．我々は，くり込みの流れ（図1）を元にしたより一般的な議論により，二つの固定点 \(X, Y\) での \(\lambda\) のスケーリング次元，\(y_\lambda < 0\) と \(y_\lambda^\prime > 0\) を用いて，\(\nu\) と \(\nu^\prime\) との間に，$$\frac{\nu^\prime}{\nu} = 1 – \frac{y_\lambda}{y_\lambda^\prime}$$という関係式が成立することを示した．

また，提案したスケーリング関係式が成立していることを確認するために，平均磁化の方向に依存したスピン揺らぎのフーリエ変換 \(\tilde{S}_k\)を定義しその振る舞いをモンテカルロシミュレーションにより計算した．この \(\tilde{S}_k\) は有限サイズスケーリング $$\tilde{S}_{k} \sim L^\mu g \left [(T-T_c)L^{\nu^\prime}\right]$$ に従うことが期待される．図2 に示したように，数値計算結果は，期待される有限サイズスケーリングによく従っており，我々が提案したスケーリング関係式が確かに成立していることが確認できた．

(by 大久保 毅)

参考文献

1. T. Okubo, K. Oshikawa, H. Watanabe and N. Kawashima: Phys. Rev. B 91, 174417 (2015).
2. Y. Ueno and K. Mitsubo: Phys. Rev. B 43, 8654 (1991).
3. M. Oshikawa: Phys. Rev. B 61, 3430 (2000).
4. J. Low, A. W. Sandvik, and L. Balents: Phys. Rev. Lett. 99, 207203 (2007).