通常SU(2)の対称性をもつハイゼンベルクモデルは,モデルハミルトニアン中の 演算子「S」をSU(N)の生成子であると読み替えるだけでSU(N)の対称性をもった モデルに拡張される.この非常に単純で基礎的なモデルは,Nの値や,SU(N)の表現 を変えることによって,その基底状態が驚くほど変化するという理論的な予言が 2次元の場合になされている.ここで表現をかえるというのは,通常のSU(2)ハイゼンベルクモデルの場合のスピンの大きさを変えることに相当している. 表現を変えると基底状態が変わるというのは1次元の場合にSの偶奇によって励起に ギャップがあるかどうかの問題(ハルデーン問題)としてよく知られているが, 2次元に関しては具体的に調べられたことがない.われわれはこれを量子モンテカルロ法で, 新しく考案したアルゴリズムを用いて計算し,最も簡単な表現を用いた場合には Nが4以下で基底状態はネール状態,5以上では自発的に空間的並進対称性がやぶれた 「ダイマー状態」が出現することを見出した.図1はその概念図であり,濃い色の線は その部分にあるスピン対がより強い相関を持っていることを表している.

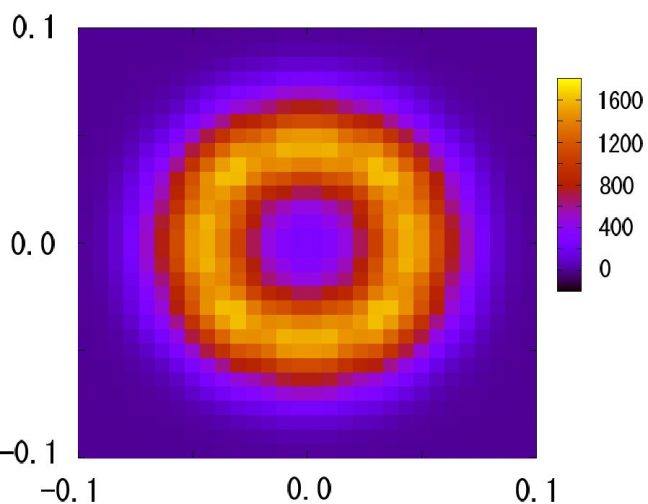
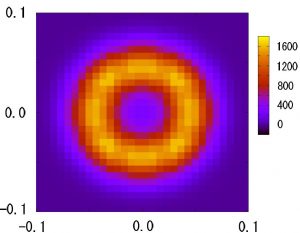
さらにこのダイマー基底状態の空間には近似的なU(1)対称性があることを見出した. 図2は横軸にX方向のダイマー秩序変数,縦軸にY方向のダイマー秩序変数をとって分布関数を示したもので,これが円に近いことがこの近似的対称性を反映している. さらに基本表現以外の場合には,空間構造が現れにくいことも分った.
(by 川島直輝)
参考文献
- Kenji Harada, Naoki Kawashima and Matthias Troyer: “Neel and Spin-Peierls ground states of two-dimensional SU(N) quantum antiferromagnets”, Phys. Rev. Lett. 90 117203-117206 (2003).
- Naoki Kawashima and Yuta Tanabe: “Representation-Dependent Ground-States of the SU($N$) Heisenberg Model”, Phys. Rev. Lett. 98 057202(1-4) (2006).