量子多体系の大規模計算によって解明が期待できる問題は数多く残されている。 近年のハイパフォーマンス・コンピュータは、京コンピューターに代表されるように、多数コアによる大規模並列により計算性能を稼ぐものが主流であり、大規模計算を行う場合、アルゴリズムの並列化が有効な手段として挙げられる。ファインマンの経路積分表示に基づく世界線量子モンテカルロ法は比較的大きなサイズの量子多体系を統計誤差の範囲内で精密に計算できる数値計算手法であるが、中でもワームアルゴリズム[1,2]は、大域的な更新ができる、汎用性の高い優れたアルゴリズムである。 しかし、ワームアルゴリズムでは、空間の1点に着目し、そこに挿入されたワームと呼ばれるオペレーターがループを描きながら世界線の状態を更新していく、イベント駆動型であることから、並列化が非自明である。
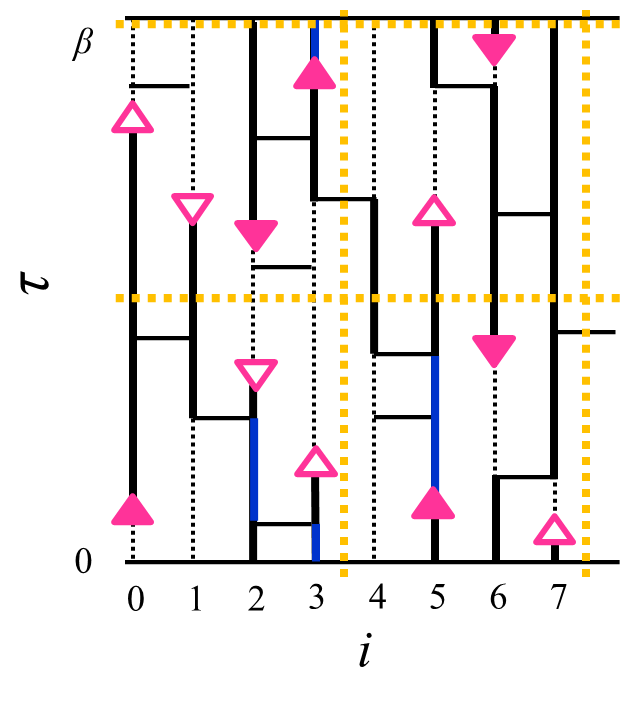
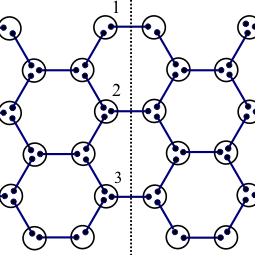
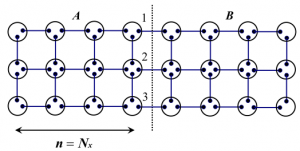
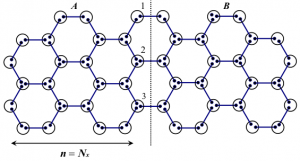
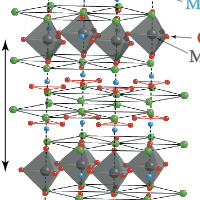
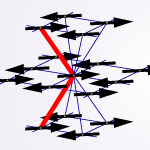
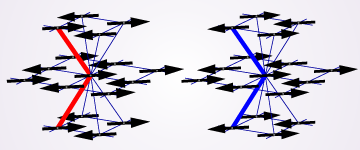
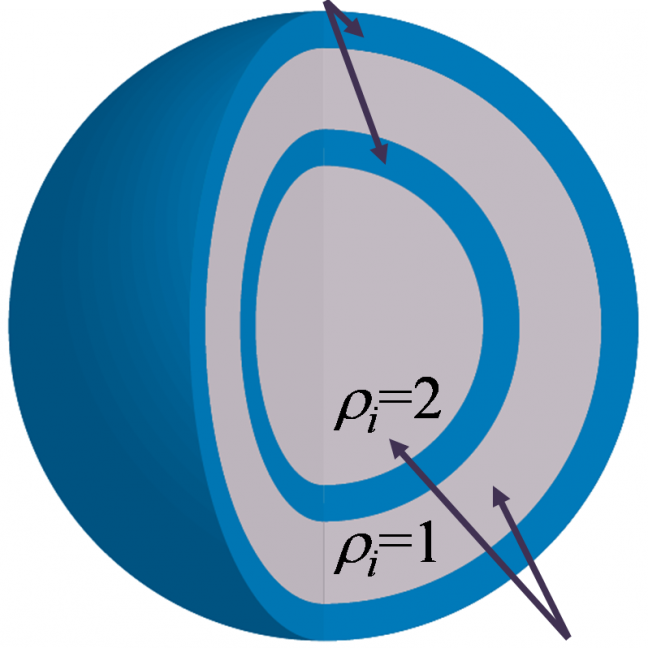
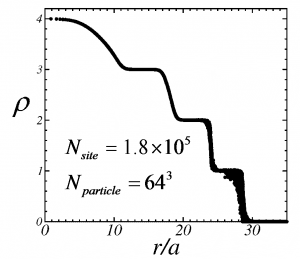
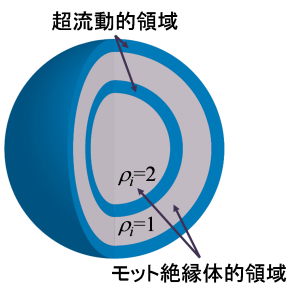
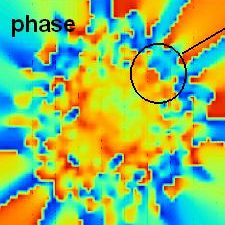
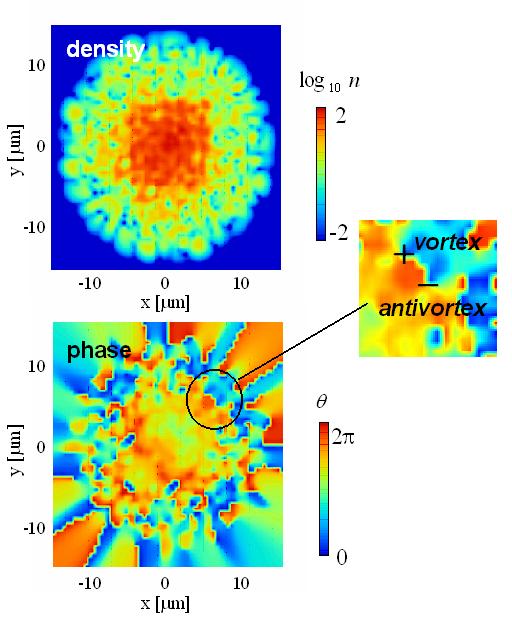
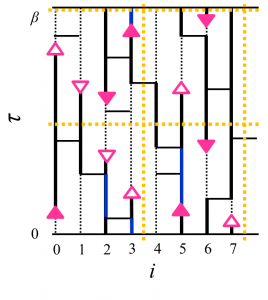
我々は向き付きループアルゴリズム(DLA)[2]に基づき、複数のワームを配位空間中に挿入でき、配位空間をドメイン分割できる並列計算向きのアルゴリズム(Parallelized Multi-Worm Algorithm = PMWA)を考案した(図1)。複数ワームはモデルハミルトニアンにソース場ηを付加し調節することにより導入され、測定された物理量をη=0の極限に外挿することによってソース場のない時の結果が得られる。ワームを複数扱う際には、これまでのワームアルゴリズムと同じ手続きでは時間反転対称性を満たすように状態更新がでないが、我々のアルゴリズムはこれを満たすようにできている。また、ドメイン間通信によりワームのドメイン間移動とドメイン境界の状態更新が有効的に果たされ、エルゴード性も保たれている。この際の情報転送量はドメイン表面積にしか依存しないため、プロセッサ並列数が増えても高い並列化効率を維持することができる。 このアルゴリズムはこれまでのワームアルゴリズム同様、ソフトコア・ボーズ粒子系や、不符号問題のない量子スピン系に適用できる。
我々はこのアルゴリズムを正方格子上拡張ハードコア・ボーズ・ハバードモデル
![]()
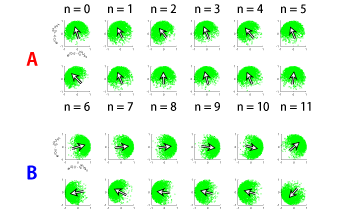
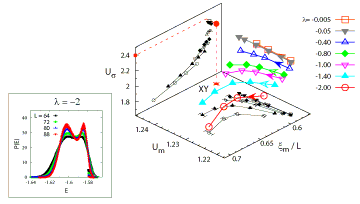
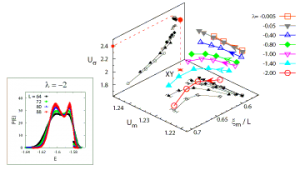
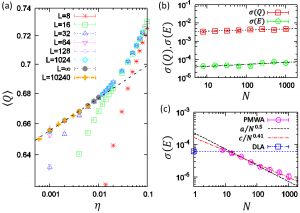
に適用し、ベンチマーク計算を行った。 ここでiサイトのボゾンの消滅(生成)演算子を bi (bi†)とし、 tは隣接サイト間の粒子のホッピングエネルギー、Vは隣接サイトの粒子間相互作用、μは化学ポテンシャルをそれぞれ表している。我々は物理量のηに関する外挿則を導き、DLAの結果と比較することで、物理量がそれに従い振る舞うことを確認した。 図2(a)は超流動相でのボーズ・アインシュタイン凝縮秩序変数Qをηの関数としてプロットしたものである。ここではLを一方向あたりの全格子数、βを逆温度としたとき、最大でL×L×β =10,240×10,240×16のサイズの計算を3,200プロセッサ並列により実現した。 これはシングルプロセッサの計算で実行できるサイズを大きく上回っている。 また、我々はアルゴリズムの精度を評価するために、標準誤差のドメイン分割数Nの依存性を調べた。 分割による緩和速度の低下は非常に小さいことがわかった(図2(b))。 また、ストロングスケーリングでの並列化効率が非常に良いために、同じ実時間内で従来のアルゴリズムと比較した場合、 N>8で従来のアルゴリズムの精度を上回り、Nを上げるにつれさらに精度が向上することを確認できた(図2(c))。
参考文献
[1] N. Prokof’ev, B. Svistunov and I. Tupitsyn, Sov. Phys. JETP 87, 310 (1998) 等.
[2] O. F. Syljuasen and A. W. Sandvik, Phys. Rev. E 66, 046701 (2012).
[3] A. Masaki-Kato, T. Suzuki, K. Harada, S. Todo and N. Kawashima, Phys. Rev. Lett. 112, 140603(2014).