スピングラス問題はランダム磁性体の実験において発見され,その後この現象を説明するためにエドワーズ・アンダーソン模型が提案された.以来,このモデルの単純さと問題の根源的な性質のために,スピングラス問題研究のために多大な努力がなされた.我々はモンテカルロシミュレーションによって3次元系の場合の相転移の存在を確認したが [1],スピングラス相の基本的な性質に関する議論は,今日でもまだ決着を見ていない.これについては,初期の理論的な研究から2つのパラダイム — 平均場描像とドロップレット描像 — が提案されている.この20年の研究は3次元スピングラスに対して,どちらの描像が正しいか,という点に集約される.初期の段階から,数値計算はこの問題解決の基本的なアプローチであったが,この問題が数値計算の観点からも困難であることはすぐに明らかになった.スピングラス問題に関する数学的に厳密な命題すら存在している.すなわち,3次元以上でエドワーズ・アンダーソンモデルの基底状態を求める問題はNP困難である.今日,最速の計算機で,基底状態を求められる問題の最大サイズは一辺の長さが L=30 を超えず,これは,問題を疑問の余地なく解決するには足りない大きさである.
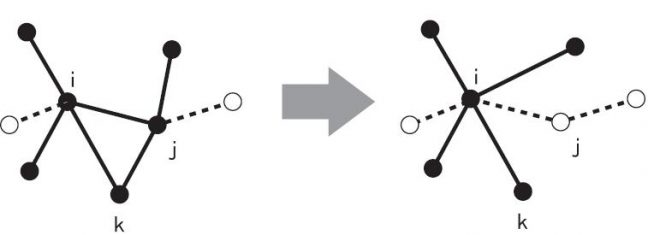
そこで,我々は問題に対する別のアプローチを考えた[2].すなわち,再帰的な変形により,問題を近似的に解く方法である.このタイプのアプローチでもっとも良く知られているのは,ミグダル・カダノフ(MK)による実空間繰り込み法である.この方法は強磁性イジングモデルに対して,かなり正確な答えを与え,後にスピングラス問題に対しても応用された.我々の方法では「縮約」操作を繰り返し問題に適用することで答えが得られる.図1に示されるように,縮約はボンドの繋ぎかえと,それに伴うボンド強度の再計算からなる.問題が定義されている有限サイズの格子からスタートして,この縮約操作によって次第に格子をループを含まないグラフ(=ツリー)へと変形していくのがこの方法のエッセンスである.一旦,ツリー上の問題に変形されてしまえば,その問題に関して厳密な物理量を計算することは易しい.このやり方で,我々は近似なしには到達できないサイズの系の計算を行うことができる.
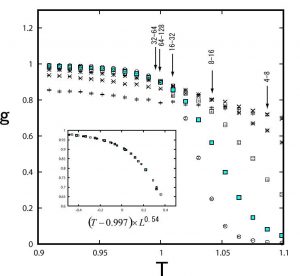
この方法を用いて我々はさまざまな物理量を計算した.たとえば,3次元系ではスピングラス帯磁率がある温度で急激な変化を示し,この温度付近で転移があることに対応している.図2はビンダーパラメータの温度依存性をさまざまなサイズについて示したもので,異なるサイズに関する曲線が交わる点が転移温度を与える.交点から \(T_c = 1.0 J\),\(g_c = 0.9\) という評価が得られる.挿入図はその有限サイズスケーリングであり,ここから,臨界指数 \(\nu\) について \(\nu = 1.85\) という評価が得られる.これらの値は近似を用いない,最新のモンテカルロシミュレーションの結果 \(T_c = 0.98(5)\) , \(\nu = 2.00 (15)\) に近い値であり,用いている近似の「乱暴さ」から考えるとむしろ不思議なほど一致している.また,MK近似から得られた値 [4] \(T_c = 0.39\) and \(\nu=2.8\) に比べても良い.
オーバーラップの分布関数に有限の幅があるかどうかが,上述の2つのパラダイムのどちらが正しいかの判定条件の1つになっている.我々の近似は幅がゼロであることを示し,ドロップレット描像と整合性のある結果を導くが,近似のためである可能性があり,これをもってドロップレット描像が正しいと結論を下すことまではできない.
(by 川島直輝)
References
[1] N. Kawashima and A. P. Young: “Phase transition in the three-dimensional ±J Ising spin glass”, Phys. Rev. B 53 (1996) R484.
[2] N. Kawashima: “Tree approximation for spin glass models”, J. Phys. Soc. Jpn. 25 (2006) 073002.
[3] E. Marinari, G. Parisi and J. J. Ruiz-Lorenzo: “Phase structure of the three-dimensional Edwards-Anderson spin glass”, Phys. Rev. B 58 (1998) 14852.
[4] B. W. Southern and A. P. Young: “Real space rescaling study of spin glass behavior in 3 dimensions”, J. Phys. C 10 (1977) 2179.