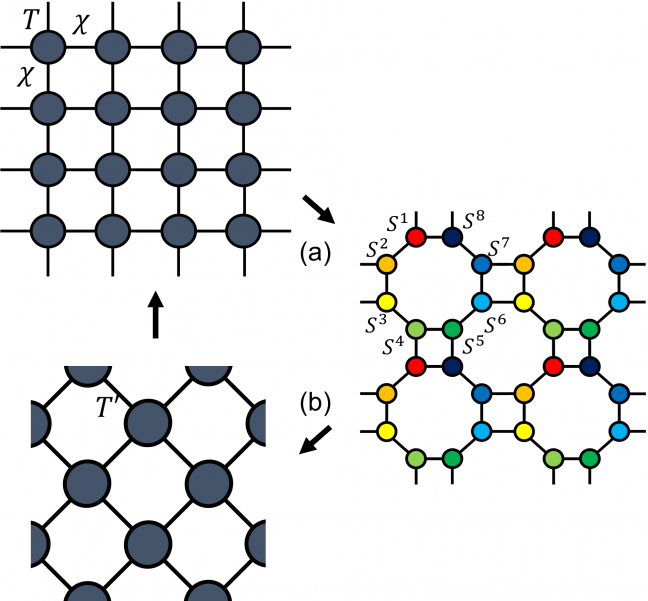
テンソルネットワーク法は、量子系および古典系の多体問題を解く上で有効な計算手法と信じられている。しかし、多体系に対するテンソルネットワークAnsatzの表現能力に対する理解は、ループのないテンソルネットワークに限られている。ループのないテンソルネットワークの場合、カノニカルゲージを導入することで効率的に多体問題を解くことができる [1]。しかし、文献. [2]で議論されているように、ループのあるテンソルネットワークに対しては、前述の手法を適応することができない。そのため、ループのあるテンソルネットワークに対する効率的で計算量の少ない最適化手法を開発することは、依然として困難な課題であることが知られていた。
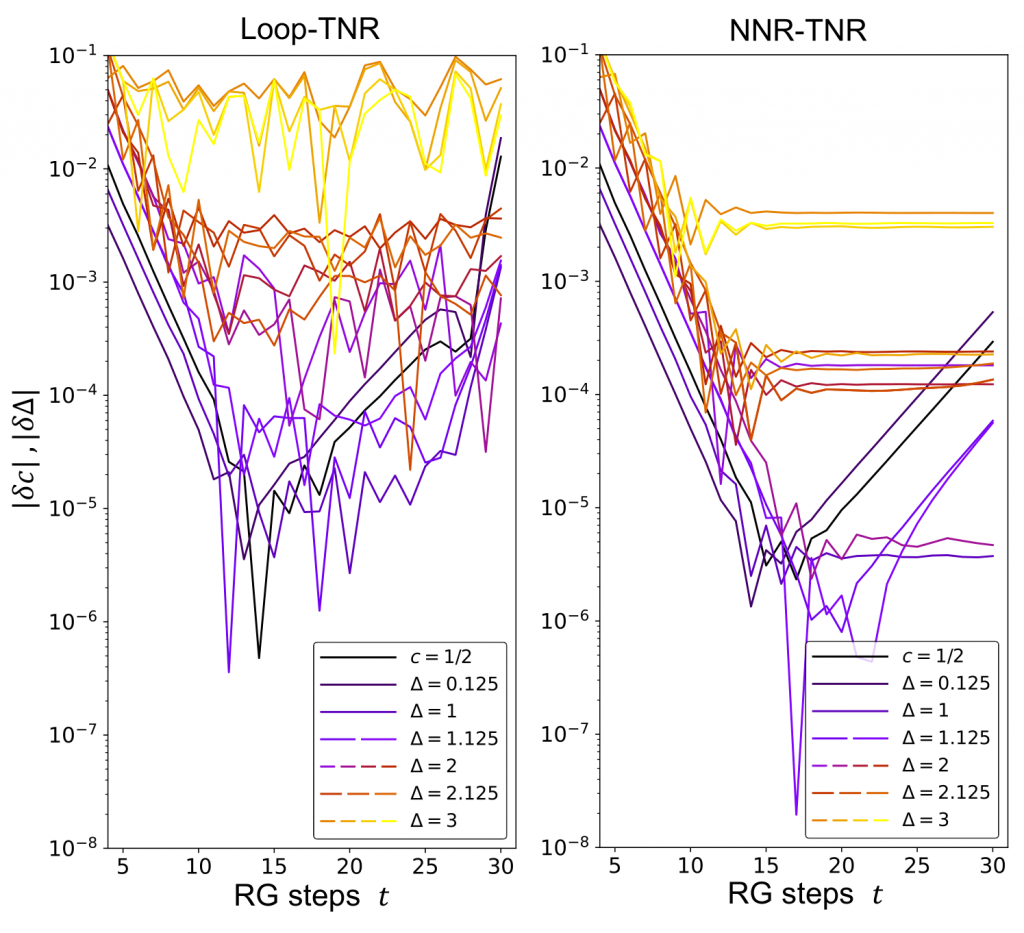
本論文では、核ノルム正則化 [3]と言われるデータ処理分野のアイディアを応用することで、短距離相関に起因する局所的な極小値を回避するループ最適化アルゴリズムを提案した。我々は、臨界2次元イジングモデルを題材にして、テンソル繰り込み群 [4]の一部に核ノルム正則化を導入することで、本手法の性能を検証した。結果として、繰り込まれた固定点テンソルのスケール不変性がより高い精度で実現され、スケーリング次元スペクトルの高次の部分がより安定に求められることが分かった [5]。
[1] G. Vidal, Efficient classical simulation of slightly entangled quantum computations, Phys. Rev. Lett. 91, 147902 (2003).
[2] G. Evenbly, Gauge fixing, canonical forms, and optimal truncations in tensor networks with closed loops, Phys. Rev. B 98, 085155 (2018).
[3] M. Jaggi, M. Sulovsk et al., A simple algorithm for nuclear norm regularized problems, in Proceedings of the 27th International Conference on Machine Learning (ICML-10) (ACM, New York, 2010), pp. 471–478.
[4] S. Yang, Z.-C. Gu, and X.-G. Wen, Loop optimization for tensor network renormalization, Phys. Rev. Lett. 118, 110504 (2017).
[5] K. Homma, T. Okubo, and N. Kawashima, Nuclear norm regularized loop optimization for tensor network, Phys.Rev. Res. 6, 043102 (2024).