作者別: Tateki Obori

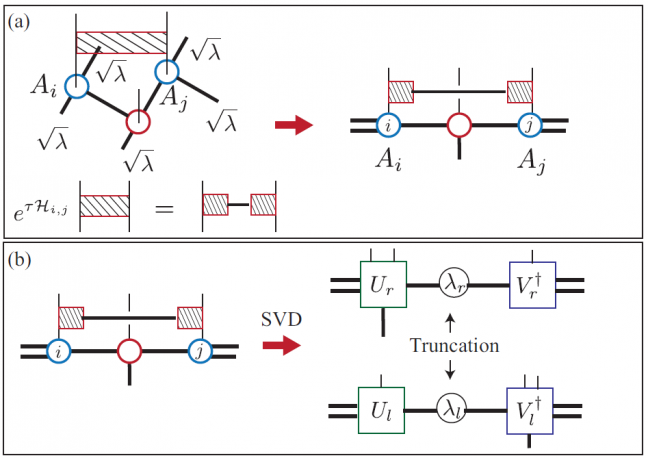
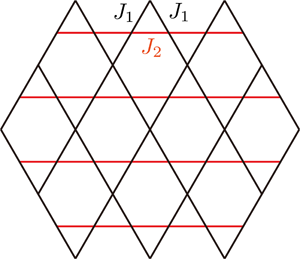
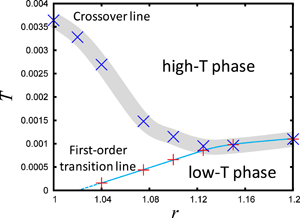
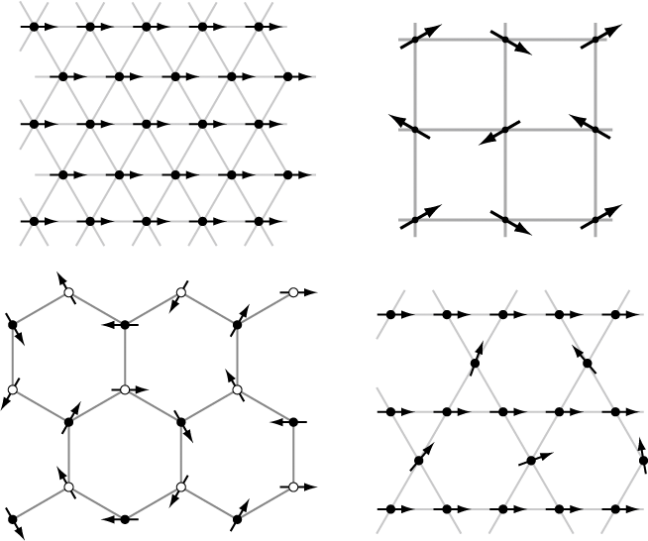
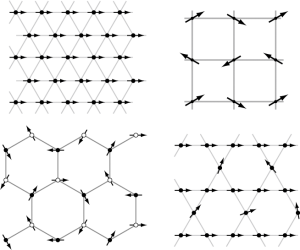
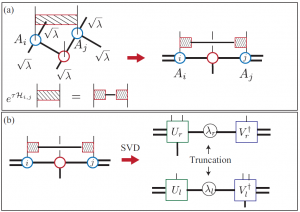
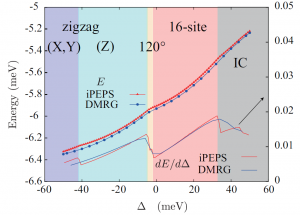
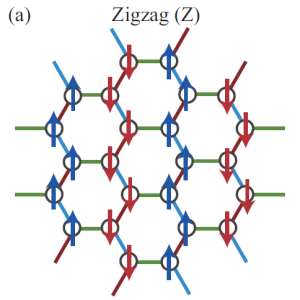
トポロジーによって特徴づけられる量子状態の研究が盛んにおこなわれているが，キタエフモデルはそのような状態を基底状態として持ち，かつ厳密に解けるモデルである．キタエフモデルは非常に人工的なモデルであるために，現実の物質でこれに対応するものが存在するかどうかに関心が集まっている．Jackeli と Khaliullin [1] はスピン軌道相互作用が強い物質においては，キタエフモデル的相互作用が重要になることを指摘し，スピン軌道相互作用が大きなイリジウム原子を含んだNa2IrO3などの化合物が候補物質とされた．山地ら [2] は第一原理計算に基づいて，Na2IrO3 の磁性に関する有効モデルを提案した．このモデルは，ハチの巣格子上のキタエフモデルのハミルトニアンに，ハイゼンベルク項や，異方性を表す項などを付け加えたものになっているが，フラストレーションを持つスピン系であるために，通常の量子モンテカルロ法では基底状態の信頼できる計算が不可能である．我々は，このモデルをテンソルネットワーク法などで取り扱った．[3] このモデルでは，相互作用が最近接だけでないために，テンソルの最適化に際して，特別な更新手法を工夫した．（図１）これによる計算の結果，三方晶ゆがみの大きさを自由パラメータとした１次元相図を描いた．（図２）この結果，Na2IrO3に相当する点においては，図１に示されるようなパターンをもった磁化秩序相であることが示された．これは，小さなクラスタの厳密対角化計算による先行研究の結果を支持する．Na2IrO3に相当する点から離れた領域においては新たに３つの相の存在を見出した．第１に，３分の１の六角形において互いに１２０度の向きにそろった磁化をもつ１２０度磁気秩序相，第２に，１６サイトで１つのユニットセルを作る磁気秩序相，第３に格子の周期とは，非整合な周期をもつ非整合磁気秩序相である．

この結果は，A2IrO3型の磁気化合物が多彩な磁気秩序相を示すであろうことを示唆しており，スピン液体状態の探索にも有用な知見を与えるものである．また，従来は，小規模系の厳密対角化で我慢するしかなかったフラストレート量子スピン系の研究にテンソルネットワーク法が加わったことによって，今後多くの未解決問題に信頼できる解が与えられるものと期待される．

(by 川島 直輝)

[参考文献]

[1] G. Jackeli and G. Khaliullin, Phys. Rev. Lett. 102, 017205 (2009).

[2] Y. Yamaji, Y. Nomura, M. Kurita, R. Arita, and M. Imada, Phys. Rev. Lett. 113, 107201 (2014).

[3] Tsuyoshi Okubo, Kazuya Shinjo, Youhei Yamaji, Naoki Kawashima, Shigetoshi Sota, Takami Tohyama, and Masatoshi Imada, Phys. Rev. B 96, 054434 (2017)

カゴメ格子は，三角形が頂点を共有して結合した二次元のネットワークであり（図１），相互作用が競合する幾何学フラストレーションの典型的な舞台となっている．例えば、カゴメ格子上で最近接相互作用する古典ハイゼンベルグ反強磁性体では，格子の強いフラストレーションにより基底状態が大規模に縮退しており，その磁気的な秩序化には多くの興味が持たれてきた．近年，このようなカゴメ格子反強磁性体と良く近似できる物質として，ハーバートスミス石，ボルボース石，ベシニエ石（ZnCu₃(OH)₆Cl₂，Cu₃V₂O₇(OH)₂， BaCu₃V₂O₈(OH)₂）といった銅鉱物が注目され，実験的に盛んに研究されている[1]．しかし，これらのうち，ボルボース石，ベシニエ石では，カゴメ格子はわずかに歪んでおり，この格子歪みが磁気秩序化に与える影響についての理論的な解析が期待されていた．

我々は，格子の歪みによるスピン間の交換相互作用の変化を考慮し，図１の様に，カゴメ格子上の一軸方向の交換相互作用J₂がその他の相互作用J₁と異なる，歪んだカゴメ格子上の古典ハイゼンベルグスピン系の秩序化を，モンテカルロシミュレーションにより解析した．その結果，歪みの効果により，歪みの無いカゴメ格子では見られなかった新しい一次相転移が，交換相互作用 J₁と比べて0.1％以下のごく低温で生じることが明らかとなった[2]．この一次相転移には，スピンが作るベクトル・カイラリティのドメイン壁や，Z₂渦と呼ばれる特殊な渦励起といった，トポロジカルな励起が関係していることが示唆されており，フラストレート磁性体における新奇な秩序化機構が起源となっている可能性がある．

（by 大久保毅）

[参考文献]

[1] P. Mendels and F. Bert, J. Phys. Soc. Jpn. 79, 011001 (2010), Z. Hiroi, et al, J. Phys.:Conf. Ser. 320, 012003 (2011), Y. Okamoto, J. Phys. Soc. Jpn. 78, 033701 (2009).等

[2] H. Masuda, T. Okubo, and H. Kawamura, Phys. Rev. Lett 109, 057201 (2012).

XY モデルやハイゼンベルクモデルなど連続的な自由度を持つスピン系では、2次元空間で長距離秩序が実現されないことが知られている。ただし、長距離秩序が実現されないのは系の相互作用が短距離であることを仮定した場合であって、相互作用が長距離であるときには長距離秩序を示すこともある。長距離相互作用があるスピン系の研究は、スピンの数の増大とともに計算量が急激に増大することから、これまであまりなされてこなかった。しかし最近提案されたオーダーNモンテカルロ法[1]により短距離相互作用のときと変わらない計算量で長距離相互作用するスピン系の計算が可能となった。

そこで我々はオーダーNモンテカルロ法を用いて2次元格子上のハイゼンベルク双極子の計算を行った。扱った格子は三角格子、正方格子、ハニカム格子、カゴメ格子の4種類で、それぞれの格子における相転移について調べた。それぞれの秩序相は右図の通りで、三角格子では強磁性、正方格子では反強磁性、ハニカム格子では渦構造、カゴメ格子では部分的な強磁性秩序が見られた。それぞれの相転移は、ハニカム格子でコスタリッツ・サウレス転移が、それ以外の格子では2次相転移が観測された。相転移点近傍における磁気異方性を計算したところ、正方格子と三角格子では、エントロピーの効果によって特定の向きが安定化される「無秩序による秩序」と呼ばれる現象によって秩序を形成していることが分かった。一方、ハニカム格子では相転移温度以下においても磁気異方性はなく、スピンが”丸い”まま秩序を形成していることが明らかとなった。またカゴメ格子では、相転移温度以下においても秩序化しないスピンが存在していることから、系は強磁性を示しつつも無数の状態を取りうる残留エントロピーを有している可能性が示された[2]。

（by 富田裕介）

[参考文献]

[1] K. Fukui and S. Todo: “Order-N cluster Monte Carlo method for spin systems with long-range interactions”, J. Comput. Phys. 228 (2009) 2629.

[2] Yusuke Tomita: “Monte Carlo Study of Two-Dimensional Heisenberg Dipolar Lattices”, J. Phys. Soc. Jpn 78 (2009) 114004.