作者別: Satoshi Morita

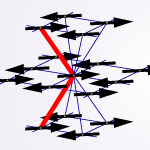
BaCuSi₂O₆ [S. E. Sebastian, et al.: Nature 441 (2006) 617]は擬2次元のスピンダイマー反強磁性体である。この物質の磁場下における低エネルギー励起を記述するハードコアボーズ模型ないしXY模型を考えると，これには面間相互作用が相殺する形の特徴的なフラストレーションがある。しかしながら揺らぎを考慮に入れるとこの相殺は不完全になり，この系の磁場中秩序相 （マグノンBEC相）への有限温度相転移は３次元的なものとなる。

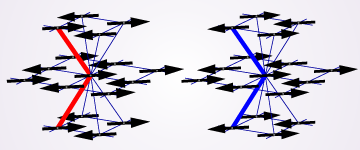
我々は，相殺しきれない面間相互作用（＝「有効面間相互作用」）の形を，有限温度相転移の有効模型となる古典系においてスピン波近似で議論した。その結果，1) 隣接面間には双二次相互作用があるが対称性のために双一次相互作用はないこと，2) 一方次近接面間には強磁性的な双一次相互作用があることが明らかになった。このことから予想される秩序状態の模式図を図1に示す。最近接面間の反強磁性モーメントが平行か反平行かのいずれかが自発的に選ばれ（Z2対称性の破れ），その配置で反強磁性の長距離秩序がおこる（O(2)対称性の破れ）。図2は実際にシミュレーションで確かめられたこの状態のスナップショットである。

このような複合的な対称性の破れの構造を持つことは相転移の普遍性クラスにどのように影響してくるのか。これについて調べるため，我々はLandau-Ginzburg-Wilson型の有効ハミルトニアンを解析し，数値計算による臨界指数の評価と比較した。その結果，転移点最近傍において，予想されていた3次元XYタイプの臨界現象から何か別のものへのクロスオーバーがあらわれることが分かった。

（by 紙屋佳知）

参考文献

Y. K., Naoki Kawashima, and Cristian D. Batista:  “Finite-Temperature Transition in the Spin-Dimer Antiferromagnet BaCuSi₂O₆” J. Phys. Soc. Jpn. 78 (2009) 094008

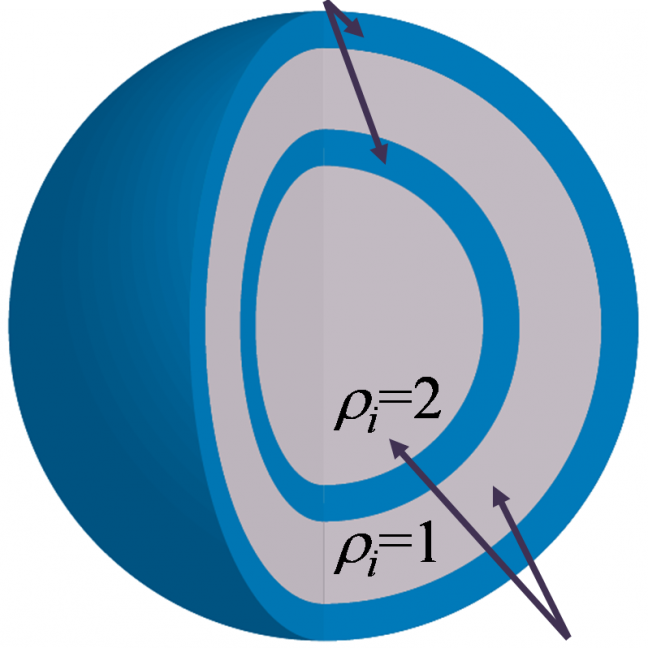
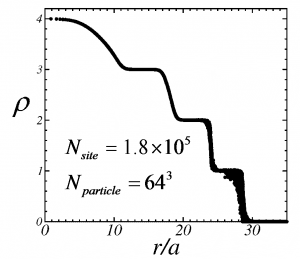
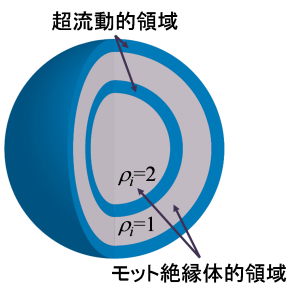
光学格子中にトラップされたボーズ粒子の有効モデルとしてボーズハバードモデルの研究が盛んに行われている． 先駆的な実験的研究では, 粒子数が2 × 10⁵個程度，格子サイズが65³程度のものを取り扱っている． 我々は向きつきループアルゴリズムの改良を行い，実験系と同規模の粒子数（1.8 × 10⁵）及びサイト数 （64³） のシミュレーションを実装した． この系には調和型のトラップポテンシャルが存在し， これによりトラップの中心から離れるに従って，各サイトのボゾンの平均占有数は減少していく． また低温でt/Uが小さい場合を考えると，図１のような“ウェディングケーキ構造”と呼ばれる複数のプラトーを有する構造が実現される． このプラトーは平均占有数が整数のところに存在し，モット絶縁体的な領域が存在していると考えられる． またプラトー間には平均占有数が非整数になっている領域が存在し，位相がそろった超流動的な領域が存在していると考えられる． この超流動的な領域は図２に示すようにモット絶縁体的な領域で隔てられている． 本研究ではこの様にモット絶縁体的領域に隔てられた複数の超流動的領域間の位相の相関に着目して 計算を行った． 比較的大きな系のシミュレーションの結果，超流動的領域間の相関と同一領域内の相関はほぼ同じ温度で出現することが分かった．

（by 加藤康之）

参考文献

Yasuyuki Kato and Naoki Kawashima, “Quantum Monte Carlo method for the Bose-Hubbard model with harmonic confining potential” Phys. Rev. E. 79, 021104 (2009).

2次元一様系では、熱力学極限においてBose-Einstein凝縮（BEC）が有限温度下で実現しない一方、Kosterlitz-Thouless（KT）転移点以下では有限の超流動密度を持つことが知られている。しかし、この系に調和トラップポテンシャルを付加すると有限温度下でもBECが安定に存在することが指摘されている。それゆえに、この系の有限温度での振る舞いについては明らかになっていない。近年、アルカリ原子気体の擬2次元Bose気体における有限温度の振る舞いに関して、理論、実験の両面から研究が盛んに行なわているが[1-3]、多くの未解決部分があるのが現状である。

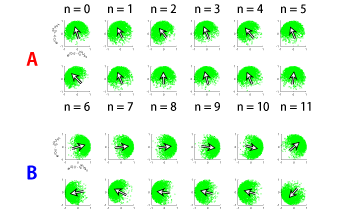
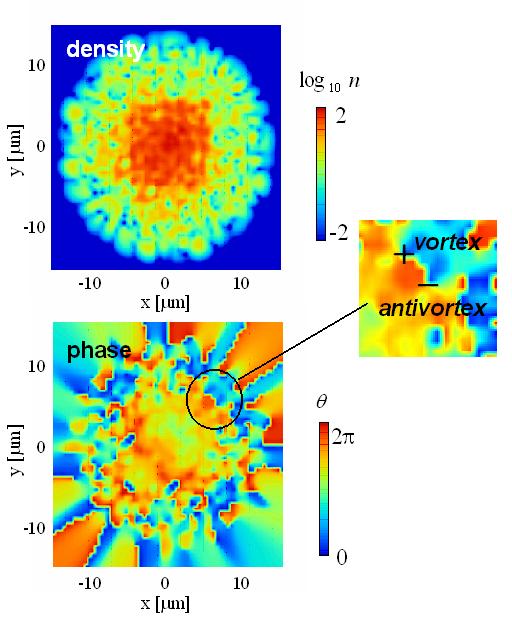
我々は、有限温度のBose気体のダイナミクスを扱うProjected Gross-Pitaevskii方程式[4]を数値的に解くことで、調和トラップ中擬2次元 Bose気体の有限温度での振る舞いについて調べた。図1は、178[nK]におけるz＝0で2次元スライスしたある瞬時の密度と位相である。この結果から、中心付近では位相がコヒーレントな領域が存在し、端付近ではvortexとantivortex の熱励起が観測された。この系における超流動出現について調べるために、系を回転させて慣性モーメントの温度依存性を測定した。

その結果、超流動密度はある温度T_rot^*を境に、温度低下とともに徐々に増加することがわかった。さらに、系のコヒーレント性を見るために、様々な温度に対して位相相関関数の距離依存性を調べた。その結果、T_rot^* 近傍において距離の冪に近い減衰をし、その指数は1/4であることが観測された。また、様々な温度においてコヒーレンス領域の節近傍でも同様な振る舞いが観測された[5]。

（by 佐藤　年裕）

参考文献

[1] S. Stock, Z. Hadzibabic, B. Battelier, M. Cheneau and J. Dalibard, Phys. Rev. Lett. 95, 190403 (2005)
[2] P. Krüger, Z. Hadzibabic, and J. Dalibard, Phys. Rev. Lett. 99, 040402 (2007)
[3] T. P. Simula, M. J. Davis, and P. B. Blakie, Phys. Rev. A 77, 023618 (2008)
[4] M. J. Davis, R. J. Ballagh and K. Burnett, J. Phys. B 81, 4487 (2001)
[5] T. Sato, T. Suzuki and N. Kawashima: “Finite-temperature transition in a quasi-2D Bose gas trapped in the harmonic potential”, J. Phys.: Conf. Ser. 150 032094 (2009).

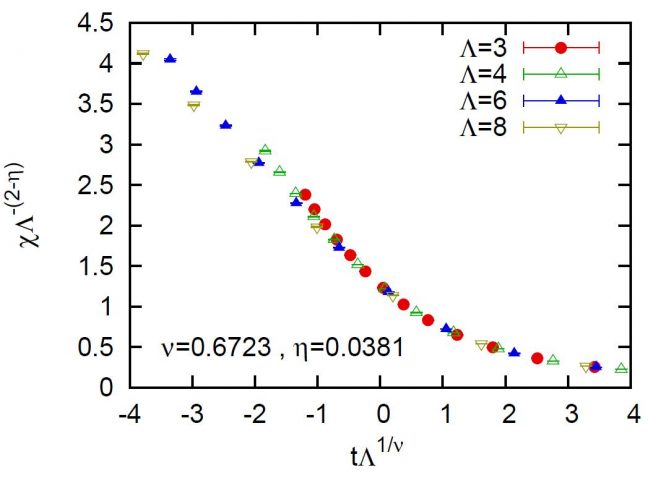
これまでにも，量子モンテカルロ法を用いて連続空間ボーズ系のシミュレーションを行った例がいくつか報告されている． しかし格子系のためのアルゴリズムが数多く報告されバリエーション豊かなのに対して，連続系のためのアルゴリズムは少数であり，それらは複雑である． 本研究では，まずはじめに連続空間のモデルを空間離散化して格子系のモデルへと変換する． そうして得られた格子系のモデルを，格子系のためのアルゴリズムを用いてシミュレートする． 連続空間ボーズ系の例として希薄ボーズ気体のモデルを用い， 格子系のアルゴリズムとして向きつきループアルゴリズム（ＤＬＡ）を用いた． ＤＬＡは既存のアルゴリズムの中でも適用範囲が広いアルゴリズムとして知られているが，ＤＬＡを今回の場合に単純に適用すると， 効率が著しく悪化する． 我々はＤＬＡに修正を加えることにより，この効率を向上させることに成功した． また実際に希薄ボーズ気体のシミュレーションを行い， 有限サイズスケーリングを用いて転移が３次元ＸＹモデルのユニバーサルクラスに属していることを確認し，転移温度の決定方法を示した． 図は感受率χの有限サイズスケーリングを示している． 指数は３次元ＸＹモデルの先行研究によって精度良く求められているものを用いている． （図中のt は相対温度（t=T-TC）, Λは系の大きさを特徴付ける長さである.）

（by 加藤康之）

[参考文献]

Yasuyuki Kato, Takafumi Suzuki and Naoki Kawashima: “Modification of directed-loop algorithm for continuous space simulation of bosonic systems”, Phys. Rev. E 75 066703(1-8) (2007).