作者別: Shumpei Iino

平衡統計力学の教科書を紐解くと、「1次元古典系では有限温度での自発的対称性の破れは存在しない」ことの証明を見つけることができる。
つまり、1次元古典系は多体問題としてほとんどつまらない。
では孤立した1次元古典系ではなく、2次元古典系の表面、すなわち2次元のバルクと接触した1次元系を考えてみることにすると、単純な1次元系とは異なる振る舞いが観測できることがある。
とりわけバルクが臨界状態である場合には、その強い相関が表面における秩序の発達を扶翼し、様々な表面臨界現象が観測されることが知られている。
その最たる例は2次元古典3重臨界イジング模型であり、バルクを3重臨界点にfine tuningして表面の温度を変化させると、1次元表面に自発磁化を生じる有限表面温度相転移が観測される[1]。
また、表面に磁場を作用させることでさらなる表面相転移が起きることも知られており、単純な古典1次元系には見られない多彩な相転移現象が展開される。

一方で、2次元臨界古典系の表面相転移現象は境界共形場理論（Boundary conformal fieled theory; BCFT）による記述が有効である。
共形不変性の制限から、可能な境界状態の完全な分類が可能となる場合もあり、さらには固定点の安定性や厳密なスケーリング次元の値を調べることができるため、表面臨界現象を詳細に理解する上で極めて重要である。

ここでは3重臨界イジング模型を対称性\(Z_2\)から\(S_3\)へ拡張した古典スピン模型である、3重臨界3状態ポッツ模型を考える。
この模型も、バルクが3重臨界点である場合に多彩な表面相転移現象を生じることがモンテカルロシミュレーションにより報告されていたが[2]、BCFTによる詳細な解析はなされていなかった。
そこで我々は、ミニマル系列境界共形場理論の\(ADE\)分類理論[3]およびテンソルネットワークくりこみ（Tensor network renormalization; TNR）[4]の手法を用いて、この模型の表面相転移を詳細に調べた[5]。

3状態ポッツ模型の3重臨界現象は中心電荷\(c=6/7\)の\(D\)型ミニマル模型に対応し、そのモジュラー不変な分配関数は\(ADE\)分類理論においてリー代数のペア \((D_4, A_6)\) で分類される。
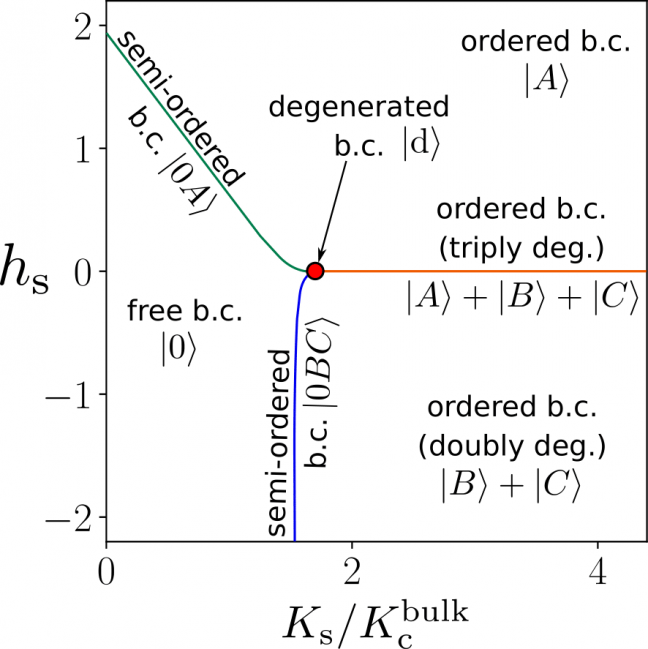
この共形場理論に対して可能な共形不変な境界状態は12個存在し（ディンキン図形\(D_4\)と\(A_6\)の頂点で特徴づけられる）、特に\(D_4\)のtrialityにより3個の\(Z_3\)対称な境界状態と9個の\(Z_3\)対称性の破れた境界状態が存在することが文献[3]の解析から導かれる。

上記の12個の境界状態をスピン模型の描像で理解するために、TNRによる数値計算を格子上の3状態希釈ポッツ模型で行った。
筆者らが提案したTNRの拡張手法により格子模型から高精度にBCFTのスペクトルを計算することができ、これを通じてBCFTで得られた境界状態と格子模型の示す相図との対応を調べることができる。
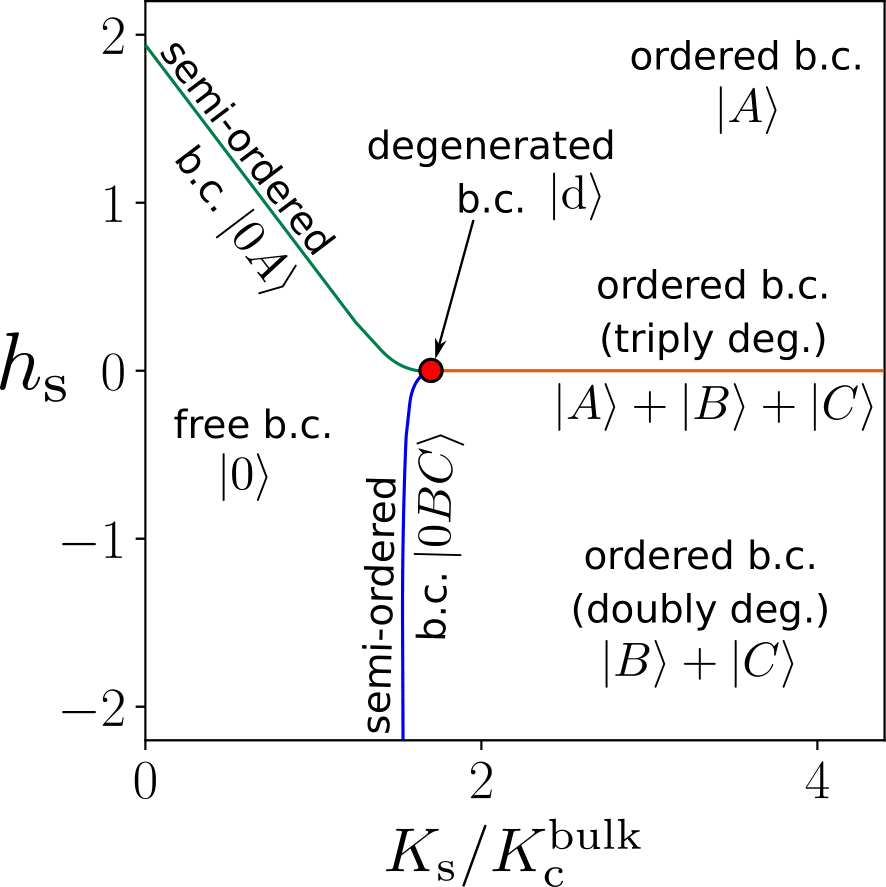
数値計算の結果、上記の12個の境界状態のうち\(Z_3\)対称な1つを除いて相図上で対応する境界状態を特定し、その物理的な意味を明らかにした（図参照）。
残った一つの境界状態は12個のうちで最も不安定な固定点に対応し、負のボルツマン重率を用いて実現されるような境界状態に対応すると予想している。
その具体的な格子模型上での実現方法を調べることは今後の研究課題である。
（by 飯野隼平）

References:
[1] I. Affleck, J. Phys. A 33(37), 6473 (2000).
[2] Y. Deng and H. W. J. Blöte, Phys. Rev. E 70, 035107 (2004); Phys. Rev. E 71, 026109 (2005).
[3] R. E. Behrend, P. A. Pearce, V. B. Petkova, and J.-B. Zuber, Nucl. Phys. B 579(3), 707 (2000).
[4] G. Evenbly and G. Vidal, Phys. Rev. Lett. 115, 180405 (2015); S. Iino, S. Morita, and N. Kawashima, Phys. Rev. B 101, 155418 (2020).
[5] S. Iino, arXiv:2007.03182; J. Stat. Phys. 182, 56 (2021).

絶対零度でも磁気秩序や対称性の破れを生じない量子スピン液体の探索は現代の物性物理学における大きな研究対象となっている。量子スピン液体を実現する方法の一つとして、スピンの高い対称性により量子揺らぎを増大することが考えられる。SU(2)対称性を持ったスピンが相互作用する通常の反強磁性ハイゼンベルグ模型において、スピンの対称性をSU(N)に拡張したSU(N)ハイゼンベルグ模型では、Nが十分に大きな極限では、バレンスボンド固体（VBS）と呼ばれる、磁気秩序が無いまま格子の並進対称性や回転対称性が破れた状態が実現することが知られており[2]、Nが小さい状況での反強磁性秩序と、Nが大きいVBS秩序との間に、スピン液体状態が存在する可能性について議論が行われている[3,4]。

我々は、このSU(N)反強磁性ハイゼンベルグ模型において、SU(N)のNの値や表現を変えた場合の基底状態について考察した。ここで、「表現を変える」ことは、通常のSU(2)スピンにおいて、スピンの大きさSを変えることに相当しており、SU(N)表現の列の数を n とすると、S=n/2 の関係が成立している。 Nが大きい領域での計算（1/N展開）では、VBS状態のパターンは、nを4で割った余りで決まり、余りが1，3の場合には、Columnar VBS（図1(a)）と呼ばれる秩序、余りが2の場合には、Nematic VBS（図1(b)）と呼ばれる秩序、余りが0の場合には、S=1の一次元スピン系のハルデーン相と同様に、対称性の破れがないVBS状態が実現すると期待されている[2]。Nがほどほどの大きさでの基底状態については、n=1の場合に量子モンテカルロ法による数値計算から、Nが4以下で反強磁性状態、5以上でColumnar VBS状態となって中間相がないとが確認されている[3,4]一方で、nが2以上の場合については、反強磁性秩序とVBS秩序の相境界については明確な結論が得られていなかった。

本研究では、並列化した量子モンテカルロ法を用いてこれまでよりも大きな系での計算を行うことで、SU(N)表現の列の数 n が2の場合には、Nが9以下では反強磁性秩序、Nが10以上ではNematic VBS秩序が基底状態となり、中間相が存在しないことを明確に示した（図2）。一方、n=3の場合には、Nが15以上で反強磁性秩序が消失する一方で、明確なVBS秩序は観測されず、中間相の存在を否定する結果は得られなかった。ただし、VBS秩序パラメタのサイズ依存性と 1/N 展開との比較から、今回の計算したシステムサイズ $L\le 128$では強い有限サイズ効果に隠れて秩序が観測されないことが示唆されるため、今回の結果は、直ちに中間相の存在を意味するものではない。将来、より大きな系（ $L\sim 500$）での計算が可能になれば、n が3以上での中間相の有無がはっきりすると期待される。

(by 大久保 毅)

[参考文献]

[1] T. Okubo, K. Harada, J. Lou and N. Kawashima: Phys. Rev. B 92, 134404 (2015).
[2] N. Read and S. Sachdev: Phys. Rev. B 42, 4568 (1990), N. Read and S. Sachdev: Nucl. Phys. B 316, 609 (1989).
[3] K. Harada, N. Kawashima and M. Troyer: Phys. Rev. Lett. 90, 117203 (2003).
[4] N. Kawashima and Y. Tanabe: Phys. Rev. Lett. 98, 057202 (2007).

層状カルコゲナイド化合物NiGa2S4は，スピン \(S=1\) の三角格子を持つ反強磁性物質であることが知られている． 近年行われた中性子散乱実験の結果から，極低温において非整合なスピン配置をとることが明らかとなっており，このことはNiGa2S4において第三近接相互作用の存在を示唆している [1,2]．

我々はNiGa2S4の有限温度の性質を調べるため，強磁性的最近接相互作用 \(J_1\) および反強磁性的第三近接相互作用 \(J_3\) のある二次元三角格子古典ハイゼンベルクモデルの解析を行った． このモデルの基底状態は非整合なスピン配置をとり，格子空間の120度回転に対応する三重縮退が存在することが分かる．（図１の模式図は基底状態のスピン配置の一例である．）

相互作用比を \(J_3/J_1=-3\) にした場合の古典モンテカルロシミュレーションを行った結果，比熱に有限温度相転移の存在を示唆する発散的なピークが一つ現れ， 転移温度において，エネルギーヒストグラムにダブルピーク構造（図２）が現れることが分かった． 得られた計算結果をもとに解析を行った結果，この系は転移温度で三重縮退した基底状態のうち一つが選ばれ，有限温度において三回対称性の破れを伴った一次相転移が存在することが明らかになった [3]．

（by 田村亮）

[参考文献]

[1] S. Nakatsuji et al., Science 309, 1697 (2005).
[2] S. Nakatsuji et al.,  J.Phys: Condens. Matter 19, 145232 (2007).
[3] R. Tamura and N. Kawashima, J. Phys. Soc. Jpn. 77, 103002 (2008).

フラストレーションの第一の効果は相殺によって相互作用を実行的に小さくすることである．準２次元系においてはフラストレーションがあると，層間の独立性を高めることになる．しかし，有限温度では，熱揺らぎの効果のために，完全な２次元性が観測されるほどの相殺が行われることはない．Maltseva と Coleman によって示されたように，ゼロ点振動の効果のために，絶対零度であっても完全な２次元性は見られない．結果として，現実の２次元系では，常に３次元系のユニバーサリティクラスの臨界現象が観測されることになる．しかし，我々は，量子臨界点近傍では，このシナリオが必ずしも当てはまらないことを見出した．[1] すなわち，量子臨界点に近付くにつれて，熱揺らぎ，量子揺らぎがともにゼロになり，漸近的に２次元性が出現することがあるのである．

この現象が最初に実験的に観測されたのは，BaCuSi2O6 における量子臨界現象である．[2]これのスピン対からなる物質のもつ高い対称性がフラストレーションの起源であり，量子臨界現象における次元効果を明らかにする上で，ユニークな特性を生み出している．この物質においては正方格子の層が互いに積層してＢＣＴ格子を作っている．各ダイマーにおける３重項のうちエネルギーの高い２つを無視することによって，この物質を，ＢＣＴ格子上の S=1/2ＸＹモデルとみなすことができる．我々は，その問題をスピン波近似でとりあつかい，マグノン励起を調べた．[1]  面間の有効相互作用は励起されたマグノンの密度に比例しており，絶対零度近傍では，純粋な２次元的振る舞いを示すことが分かった．有限温度で熱的に励起されたマグノンがもたらす面間相互作用によって，量子臨界的振る舞いから３次元的振る舞いへのクロスオーバーが発生する．特に，臨界磁場の温度依存性を特徴づける臨界指数は２次元量子系のものであり，実験と一致する．[2]

実験結果と完全な２次元系の結果は単なる定性的に一致ではなく，図２に示されるように定量的にもよく一致する．上のパネルは BaCuSi2O6  実験で観測された臨界磁場の値と量子モンテカルロ法から得られた純粋に２次元的な系の臨界磁場の値を重ねてプロットしたものである．量子モンテカルロ法で用いたモデルの結合定数は実験的に決定されたものであり，ここではフィッティングパラメータは一つもないことに注意すべきである．両方とも，漸近的には線形の振る舞いをしめし，これは，２次元量子臨界現象の特徴である．この結果は，磁化の磁場依存性（下左）や，温度依存性（下右）からも確認される．

（by 川島直輝）

[参考文献]

[1] C. D. Batista,  J. Schmalian, N. Kawashima, P. Sengupta, S. E. Sebastian, N. Harrison, M. Jaime and I. R. Fisher, Phys. Rev. Lett. 98, 257201 (2007).
[2] S. E. Sebastian, N. Harrison, C. D. Batista, L. Balicas, M. Jaime, P. A. Sharma, N. Kawashima and I. R. Fisher, Nature 441, 617 (2006).