相互作用が確率的に分布したスピングラス模型は,1975年に提案された Edwards-Anderson 模型を起源とし,ランダムネスとフラストレーションが磁気構造に与える影響について古くから盛んに研究されている.現在では,2次元ランダムボンドイジング模型の相転移点が Kitaev による量子トーラス符号の誤り訂正限界とも関連付けられるなど,統計力学以外の分野からも興味が持たれている.スピンの向きに対する熱平均と相互作用の強さに対する配位平均の2重の平均操作があるため,解析的な計算は困難であり,一般のランダムボンドイジング模型の厳密解は知られていない.一方,McCoy-Wu 模型や Shankar-Murthy 模型など正方格子上で層状に乱れた相互作用を持つイジング模型では,並進対称性より転送行列が簡単に表現できるため厳密解を導出することができる.我々は Shankar-Murthy 模型を拡張した2次元層状ランダムイジング模型を考察し,絶対零度における相転移点を厳密に導出することに成功した.これはランダムボンドイジング模型における非自明な絶対零度相転移点を解析的に導出した初めての例となっている.
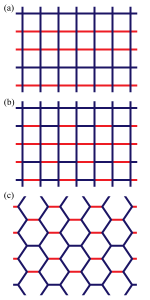
我々が考察した模型は,図1bのように水平方向に2つずらすと元にもどる並進対称性を持っており,水平方向の相互作用のみランダムで垂直方向は強磁性相互作用になっている.この模型は,周期が1の場合に相当する Shankar-Murthy 模型 (図1a) の自明な拡張となっている.垂直方向に進むの転送行列を並進対称性によりブロック対角化し,絶対零度におけるリヤプノフ指数と1次元ランダム磁場イジング模型の基底エネルギーの対応関係に着目することで,リヤプノフ指数の最大値を与えるブロックが変わる点として相転移点を導出した.確率 \(p\) で強磁性相互作用,確率 \(1−p\) で反強磁性相互作用をとる確率分布の場合,得られた強磁性相と常磁性相の絶対零度相転移確率は,正方格子と六角格子 (図1c) でそれぞれ
$$p_c^{(\text{SQ})}=\frac{\sqrt{5}−1}{2}=0.6180⋯$$
$$p_c^{(\text{HEX})}=1−2\sin\frac{\pi}{18}=0.6527⋯$$
である.
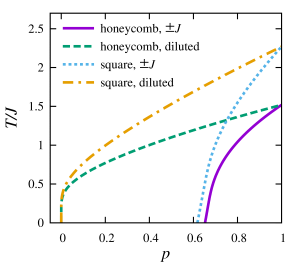
また,有限温度におけるリヤプノフ指数は,指数関数よりも早く収束するBaiの手法等を用いて数値計算することが可能である.これらの手法を用いて有限温度におけるリヤプノフ指数の交点を計算し,全領域の確率-温度相図 (図2) を高精度に決定した.
[参考文献]
[1] R. Shankar and G. Murthy: Phys. Rev. B 36, 536 (1987).
[2] S. Morita and S. Suzuki: J. Stat. Phys. 162, 123 (2016).
(by 森田 悟史)
