2次元一様系では、熱力学極限においてBose-Einstein凝縮(BEC)が有限温度下で実現しない一方、Kosterlitz-Thouless(KT)転移点以下では有限の超流動密度を持つことが知られている。しかし、この系に調和トラップポテンシャルを付加すると有限温度下でもBECが安定に存在することが指摘されている。それゆえに、この系の有限温度での振る舞いについては明らかになっていない。近年、アルカリ原子気体の擬2次元Bose気体における有限温度の振る舞いに関して、理論、実験の両面から研究が盛んに行なわているが[1-3]、多くの未解決部分があるのが現状である。
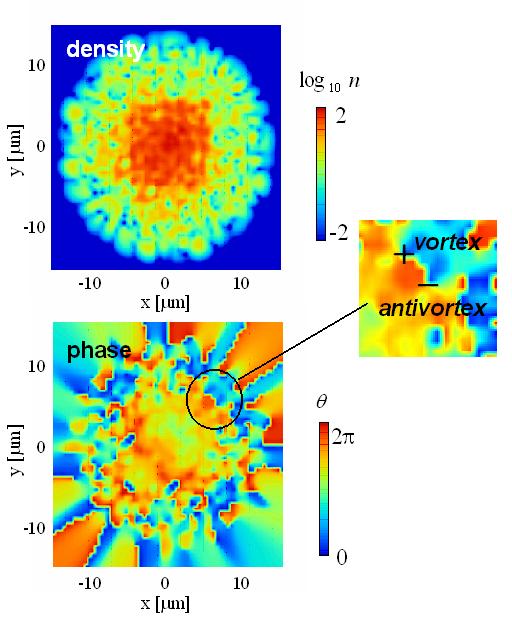
我々は、有限温度のBose気体のダイナミクスを扱うProjected Gross-Pitaevskii方程式[4]を数値的に解くことで、調和トラップ中擬2次元 Bose気体の有限温度での振る舞いについて調べた。図1は、178[nK]におけるz=0で2次元スライスしたある瞬時の密度と位相である。この結果から、中心付近では位相がコヒーレントな領域が存在し、端付近ではvortexとantivortex の熱励起が観測された。この系における超流動出現について調べるために、系を回転させて慣性モーメントの温度依存性を測定した。
その結果、超流動密度はある温度Trot*を境に、温度低下とともに徐々に増加することがわかった。さらに、系のコヒーレント性を見るために、様々な温度に対して位相相関関数の距離依存性を調べた。その結果、Trot* 近傍において距離の冪に近い減衰をし、その指数は1/4であることが観測された。また、様々な温度においてコヒーレンス領域の節近傍でも同様な振る舞いが観測された[5]。
(by 佐藤 年裕)
参考文献
[1] S. Stock, Z. Hadzibabic, B. Battelier, M. Cheneau and J. Dalibard, Phys. Rev. Lett. 95, 190403 (2005)
[2] P. Krüger, Z. Hadzibabic, and J. Dalibard, Phys. Rev. Lett. 99, 040402 (2007)
[3] T. P. Simula, M. J. Davis, and P. B. Blakie, Phys. Rev. A 77, 023618 (2008)
[4] M. J. Davis, R. J. Ballagh and K. Burnett, J. Phys. B 81, 4487 (2001)
[5] T. Sato, T. Suzuki and N. Kawashima: “Finite-temperature transition in a quasi-2D Bose gas trapped in the harmonic potential”, J. Phys.: Conf. Ser. 150 032094 (2009).