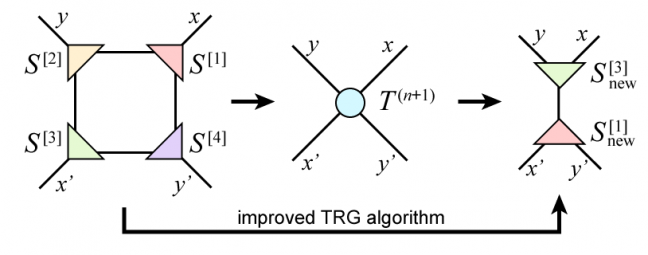
Tensor network methods are becoming powerful tools in the study of many-body problems. Real-space renormalization by coarse-graining tensor networks, including tensor renormalization group (TRG) [1] and its derivatives, is an efficient numerical method for the contraction of tensor networks. Accuracy of approximation is improved by increasing the bond dimension. However the computational complexity of TRG is proportional to the sixth power of the bond dimension \(\chi\). Thus complexity reduction without loss of accuracy is desired.
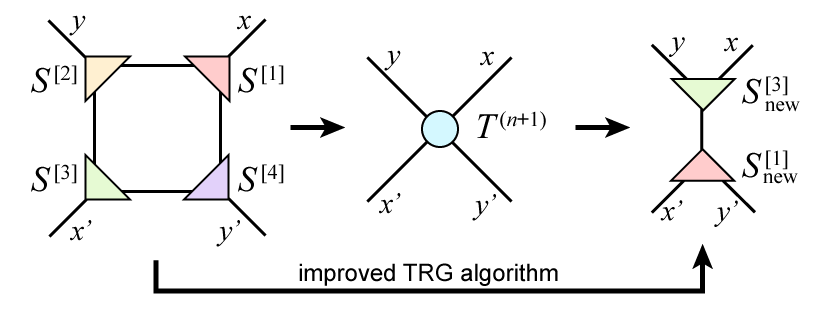
We proposed a new algorithm of TRG based on a randomized algorithm for singular value decomposition (RSVD) [2]. Its computational complexity scales as \(O(\chi^5)\). The main operations in TRG are “decomposition” and “contraction”. Since the both have \(O(\chi^6)\) complexity, we need to reduce the complexity not only by replacing the full SVD with RSVD but also by avoiding the explicit creation of a four-leg tensor. An oversampling parameter tunes the statistical error of RSVD. We showed that the oversampling parameter larger than the bond dimension reproduced the same result as the full SVD in two-dimensional Ising model. [3]
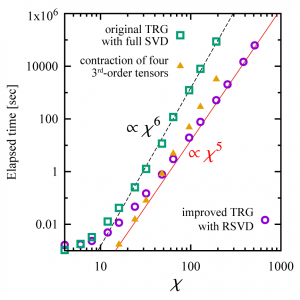
Since “decomposition” and “contraction” are dominant operations in most tensor network schemes, the techniques presented here would be useful in improving most of the tensor network calculations in an essential way.
References
- M. Levin and C. P. Nave, Phys. Rev. Lett. 99, 120601 (2007).
- N. Halko, P. G. Martinsson, and J. A. Tropp, SIAM Rev. 53, 217 (2011).
- S. Morita, R. Igarashi, H.-H. Zhao, and N. Kawashima, Phys. Rev. E 97, 033310 (2018).