Suppose we want to generate a bit string with length \(N\) in which each bit is set with arbitrary probability \(p\). If we adopt the simple algorithm, which repeats check for each bit, we need to generate \(N\) random numbers. However, we can reduce the number of random number generations by adopting more sophisticated algorithms [1]. We proposed three algorithm, the Binomial-Shuffle, the Poisson-OR, and the finite-digit algorithms.

The Binomial-Shuffle algorithm is an algorithm that first calculates how many bits are set and then shuffles them. Adopting Walker’s alias method and Floyd’s sampling method, it is possible to generate a random bit string with \(pN+1\) random number generations. The Poisson-OR algorithm generates \(k\) bit strings with one of the bits is set randomly and takes the logical OR of them. This is a special case of the algorithm proposed by Todo and Suwa [2]. The average number of the random number generations is \(-N \log(1-p)+1\). The finite digit method is effective when the probability \(p\) can be represented by a finite digit in the binary notation. When the probability p can be expressed by \(n\) digits in the binary notation, we can generate a random bit string with that probability by generating \(n\) bit strings in which each bit is set with a probability \(1/2\) and properly taking the logical operations. Therefore, the finite-digit algorithm with n digits involves the random number generates \(n\) times.
While the Binomial-Shuffle and the Poisson-OR algorithms are effective when the value of probability \(p\) is small, the required number of random numbers increases as \(p\) increases. Meanwhile, the required number for the finite-digit method does not depend on \(p\), although the method cannot be applied directly unless p can be expressed by \(n\) digits in the binary notation. Therefore, we constructed a hybrid algorithm, i.e., which first generates a bit string with probability \(\tilde{p}\) close to \(p\) with the finite digit algorithm and corrects the difference \(\tilde{p}-p\) by the Binomial-Shuffle or Poisson-OR algorithms. The expected number of random numbers generated to generate a string in which each bit is set with arbitrary probability is at most 7 for the 32-bit case and 8 for 64-bit case.
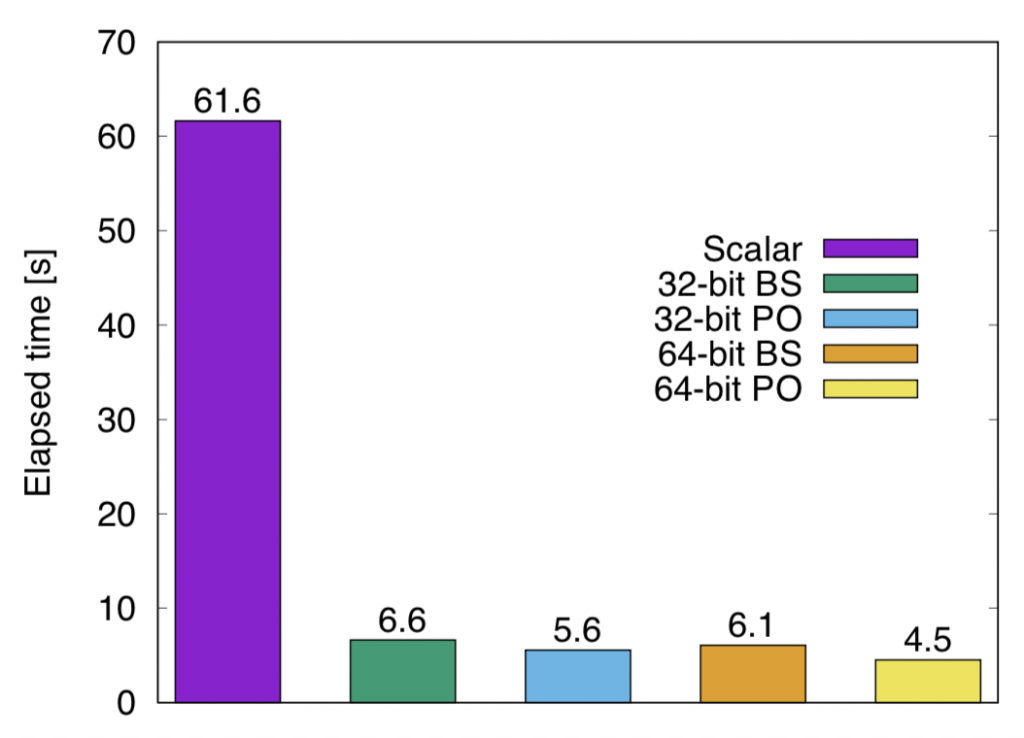
Employing the developed algorithm, we applied the multispin coding technique to the one-dimensional bond-directed percolation and obtained a factor of 14 speed-up.
References
- H. Watanabe, S. Morita, S. Todo, and N. Kawashima, J. Phys. Soc. Jpn. 88, 024004 (2019)
- S. Todo and H. Suwa, J. Phys.: Conf. Ser. 473, 012013 (2013).
