作者別: Hiroshi Watanabe

Nビットのビット列について、各ビットを確率 $p$ でランダムに1にするにはどうすればよいだろうか。単純にそれぞれのビットごとに1にするか0にするかを決めると、 $N$ 回の乱数生成が必要になる。しかし、アルゴリズムを工夫することで乱数生成回数を減らすことができる。我々はこのようなランダムなビット列を生成するアルゴリズムをいくつか考案し、それを組み合わせることで劇的に計算量を減らすことに成功した[1]。我々が提案したのはBinomial-Shuffle法、Poisson-OR法、有限桁法の三種類と、そのハイブリッド法である。

Binomial-Shuffle法は、予めいくつのビットが立つかを計算し、その後でビットをシャッフルするアルゴリズムである。立つビット数の計算にWalker’s Alias法を、ビットのシャッフルにFloydのサンプリング法を使うことで、全体で $pN+1$ 回の乱数生成でランダムビット列を生成できる。Poisson-OR法は、 $N$ ビットのうちランダムに1ビットだけビットが立っているビット列を、 $k$ 個論理和(OR)を取るアルゴリズムである。これはTodo and Suwaのアルゴリズム[2]の特殊な例になっており、ビット列の数 $k$ をポアソン分布に従うように生成することで、指定の確率でビットが立つようにできる。この手法は $-N \log(1-p) + 1$ 回の乱数生成を伴う。有限桁法は、確率 $p$ が二進数表記で有限桁で表せる場合に有効な手法である。確率 $p$ が二進数表記で $n$ 桁で表示できる場合、確率 $1/2$ でランダムにビットが立っているビット列を $n$ 個生成し、適切に論理和と論理積を取ることで、その確率でビットが1となるようにできる。したがって、確率が $n$ 桁で表現される場合、有限桁法は $n$ 回の乱数生成でビット列を生成できる。

Binomial-Shuffle法、Poisson-OR法ともに、確率 $p$ の値が小さい場合に有効だが、 $p$ が大きくなると必要となる乱数生成数が増えてしまう。そこで我々は、まず有限桁法で $p$ に近い確率 $p’$ を持つビット列を生成し、その差 $p’-p$ をBinomial-Shuffle法もしくはPoisson-OR法で補正するハイブリッド法を考案した。これにより、32ビットであればたかだか7回、64ビットでもたかだか8回の乱数生成で任意の確率 $p$ でビットが立っているビット列を生成できること示した。

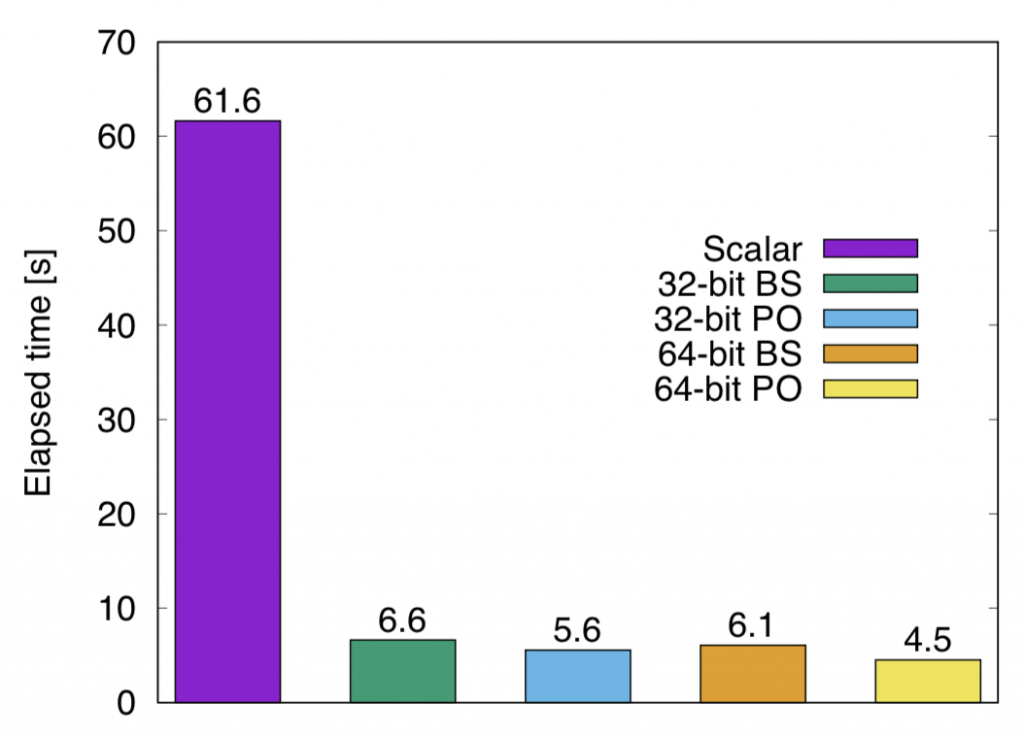
我々はこのランダムビット列生成アルゴリズムをDirected-Percolationのマルチスピンコーディングに応用し、スカラー実装に比べて14倍の高速化に成功した。このアルゴリズムは他のモデルへの応用も期待されている。

References

1. H. Watanabe, S. Morita, S. Todo, and N. Kawashima, J. Phys. Soc. Jpn. 88, 024004 (2019)
2. S. Todo and H. Suwa, J. Phys.: Conf. Ser. 473, 012013 (2013).

シャンパンや炭酸飲料の栓をあけるとたくさんの泡が出るが、その後、大きい気泡がより大きく、小さい気泡がより小さくなるOstwald成長という現象が起きる。 Ostwald成長は、合金系や液滴生成など、一次転移を引き起こす系において広く見られる普遍的な現象であり、その成長則は1960年代にLifshitz, Slyozov, Wagnerらによって完成され、LSW理論という古典論としてまとめられている[1,2]。 しかし、気泡生成現象、特に液相と気相が同じ物質である単一成分系のOstwald成長においては実験が難しく、 数値計算においても液滴生成に比べて気泡生成は要求される計算量が莫大になることからこれまで研究が進んでいなかった。 特にLSW理論で仮定されている自己スケーリング則と平均場的描像については、気泡生成系で成り立つかどうかは非自明である。

そこで我々は分子動力学法を用いた急減圧シミュレーションにより気泡分布関数の時間発展を調べた。 これまでの分子動力学法を用いた先行研究においては、泡は数個から10個程度しか表現できず、 分布関数の評価は困難であったが、京コンピュータ上で数億粒子規模の計算を行うことで、気泡分布関数を直接評価することが可能となった。 その結果、気泡分布関数が確かに自己スケーリング則に従っていること、スケーリング指数が低温では3/2、 高温では1になることがわかった。これは、気泡の成長過程が低温では界面律速であるが、高温では拡散律速にクロスオーバーすることに対応している。本研究により、気泡生成系においても自己スケーリング則が成立しており、かつ指数が古典論による予測と 一致することがわかった。これは、気泡生成過程において圧力の緩和が十分に早いため、個々の気泡が感じる圧力が一様であり、 結果として平均場描像が正当化されることを意味する。

LSW理論は、準安定領域における核生成率を予想する古典核生成論と多くの仮定を共有するが、 古典核生成論が気泡生成率の予測に失敗するのに対し、LSW理論は気泡成長を良く記述することがわかった。 古典核生成論が気泡生成率を記述できない理由については、今後の研究課題として残されている。

（by 渡辺宙志）

参考文献

[1] I. Lifshitz and V. Slyozov, J. Phys. Chem. Solids 19, 35 (1961).
[2] C. Wagner, Z. Elektrochem. 65, 581 (1961).
[3] H. Watanabe, M. Suzuki, H. Inaoka, and N. Ito, J. Chem. Phys. 141 234703 (2014).

AIPによるプレスリリース: How the Physics of Champagne and Soda Bubbles May Help Address the World’s Future Energy Needs