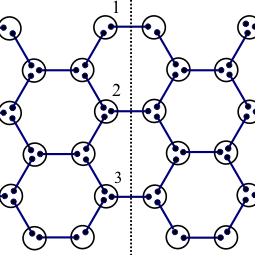
近年、量子多体系におけるエンタングルメントの定量的な研究が量子情報、物性・統計物理学の垣根を越えて盛んに行われている。 特に gapless の一次元系に関しては、エンタングルメント・エントロピーと呼ばれる指標から、 対応する共形場理論の情報が読み取れることが知られている。 また Haldane 系のように gap のある一次元系については、エンタングルメントエントロピーの飽和値と端状態の関係が、 厳密対角化や AKLT 模型を用いた解析を通じて明らかにされている。 本研究では、この端状態による解釈が二次元以上の場合にも成立するか否かを、一般のグラフ上の valence-bond-solid 状態 (VBS 状態)を用いて調べた。 二次元以上の場合には、一次元系の解析において有効である転送行列法などが使えなくなるという技術的な困難があるが、 我々はモンテカルロ法と厳密対角化を組み合わせた新しい手法を開発し、その手法を適用して正方格子および蜂の巣格子上の VBS状態でのエンタングルメントエントロピーを計算した。
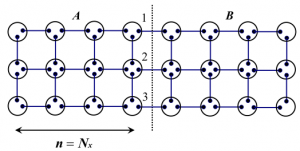
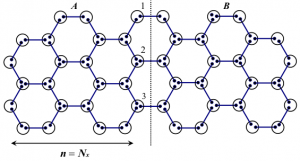
その結果、二次元以上の場合には一次元と異なり、十分大きな部分系においても 「(エンタングルメントエントロピー)=log(端状態の数)」という関係が成立せず有意な補正が生じることが明らかになった。 また正方形から成る ladder 上および、六角形から成る ladder 上におけるエンタングルメントエントロピーの値を厳密に解析した。
(by 田中宗)
[参考文献]
[1] Hosho Katsura, Naoki Kawashima, Anatol N. Kirillov, Vladimir E. Korepin and Shu Tanaka, J. Phys. A: Math. Theor. 43 (2010) 255303.