XY モデルやハイゼンベルクモデルなど連続的な自由度を持つスピン系では、2次元空間で長距離秩序が実現されないことが知られている。ただし、長距離秩序が実現されないのは系の相互作用が短距離であることを仮定した場合であって、相互作用が長距離であるときには長距離秩序を示すこともある。長距離相互作用があるスピン系の研究は、スピンの数の増大とともに計算量が急激に増大することから、これまであまりなされてこなかった。しかし最近提案されたオーダーNモンテカルロ法[1]により短距離相互作用のときと変わらない計算量で長距離相互作用するスピン系の計算が可能となった。
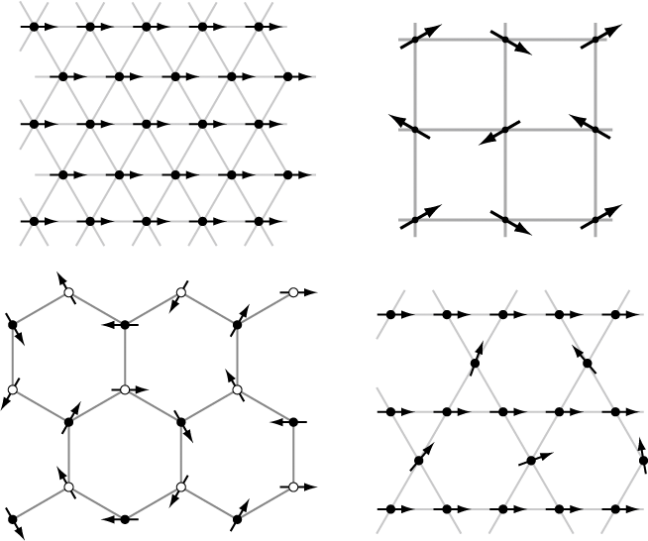
そこで我々はオーダーNモンテカルロ法を用いて2次元格子上のハイゼンベルク双極子の計算を行った。扱った格子は三角格子、正方格子、ハニカム格子、カゴメ格子の4種類で、それぞれの格子における相転移について調べた。それぞれの秩序相は右図の通りで、三角格子では強磁性、正方格子では反強磁性、ハニカム格子では渦構造、カゴメ格子では部分的な強磁性秩序が見られた。それぞれの相転移は、ハニカム格子でコスタリッツ・サウレス転移が、それ以外の格子では2次相転移が観測された。相転移点近傍における磁気異方性を計算したところ、正方格子と三角格子では、エントロピーの効果によって特定の向きが安定化される「無秩序による秩序」と呼ばれる現象によって秩序を形成していることが分かった。一方、ハニカム格子では相転移温度以下においても磁気異方性はなく、スピンが”丸い”まま秩序を形成していることが明らかとなった。またカゴメ格子では、相転移温度以下においても秩序化しないスピンが存在していることから、系は強磁性を示しつつも無数の状態を取りうる残留エントロピーを有している可能性が示された[2]。
(by 富田裕介)
[参考文献]
[1] K. Fukui and S. Todo: “Order-N cluster Monte Carlo method for spin systems with long-range interactions”, J. Comput. Phys. 228 (2009) 2629.
[2] Yusuke Tomita: “Monte Carlo Study of Two-Dimensional Heisenberg Dipolar Lattices”, J. Phys. Soc. Jpn 78 (2009) 114004.