超流動モット絶縁体転移[1]が実現して以来,光学格子中にトラップされたボーズ粒子系の研究が精力的に行われている. この系は正方格子上のボーズ・ハバードモデルによってよく記述される.
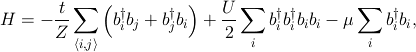
ここでi サイトのボゾンの生成(消滅)演算子を bi (bi†)とし, Z=6 は最近接のサイト数, t/Zは最近接サイト間の粒子のホッピングエネルギー, Uは同一サイトにおける粒子間の斥力相互作用をそれぞれ表している. 光学格子を形成するビームの強度を変えることにより tとUの比を調節することが可能である点で, 光学格子系は量子多体問題を取り扱うのに理想的な系であると言える. ここでは有限温度相転移を議論するため,化学ポテンシャルμ の空間的な勾配を無視し,μ/U=1/2を選び, 修正向きつきループアルゴリズム[2]を用いた量子モンテカルロシミュレーションの結果を紹介する.
図1はこの系の有限温度における相図である. 相互作用比t/Uが大きい領域では有限温度で 無秩序相から超流動相への転移が起こる. 相互作用比t/Uが小さくなるにつれて転移温度 Tcが低くなり, 量子臨界点でTc=0となる. 一方,相互作用比t/Uが量子臨界点より小さい領域では, T=0 でギャップΔが有限であるモット絶縁体相となる.
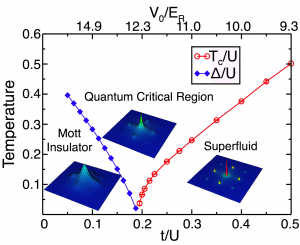
ギャップΔと相転移温度 Tc が0になる点が量子臨界点 t/U=0.192(2)である. [3]
タイムオブフライト法を用いた実験では,一方向に積分されたボゾンの運動量分布が干渉パターンとして観測される. 量子モンテカルロ法における対応する物理量は,
![]()
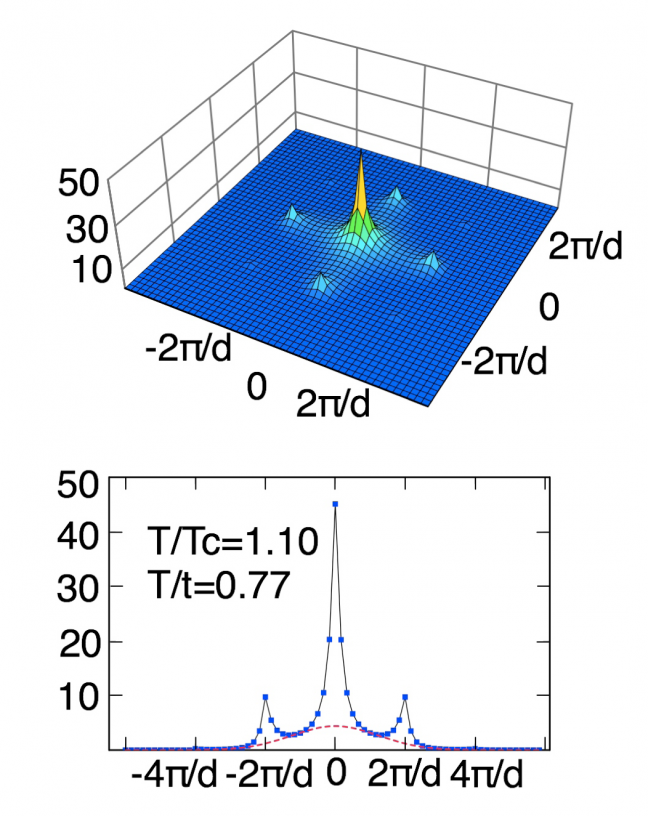
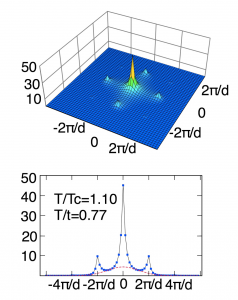
である.なお W(k) はワニエ関数のフーリエ成分であり,n(k)= Σi,j < bi† bj > exp{ik⋅ (ri –rj)}である. 図1中に3つの領域(超流動相,モット絶縁体相,臨界領域)における,典型的な干渉パターンを示した. 実験でも観測されているように超流動相では干渉ピークにシャープなピークが存在し, モット絶縁体相ではそのピークが消えていることがわかる. これまでこのシャープなピークは超流動相の指標とされてきた.図2に示したのは転移点付近の無秩序相 (t/U=0.25 ,T=1.1Tc ) における干渉パターンである. この点では超流動密度は0であり,明らかに無秩序相であるにも関わらずシャープなピークが観測されている. したがってシャープなピークは必ずしも超流動相を示すとは限らないことがわかった. 臨界温度付近の無秩序相におけるシャープなピークは,運動量0付近のピークの幅が相関長の逆数に対応していることで理解できる. 臨界点では相関長が発散するため,臨界点近くでは無秩序相であってもシャープなピークが観測される.
(by 加藤康之)
[参考文献]
[1] M. Greiner, O. Mandel, T. Esslinger, T. W. Hänsch, and I. Bloch, Nature 415, 39-44 (2002).
[2] Y. Kato, T. Suzuki, and N. Kawashima, Phys. Rev. E 75, 066703 (2007).
[3] Y. Kato, Q. Zhou, N. Kawashima, and N. Trivedi, Nature Physics 4, 617 (2008).