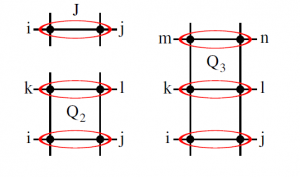
Two-dimensional SU(N) Heisenberg Model with Multi-spin Interactions

Posted on by Satoshi Morita

The quantum phase transition from the Neel order to the Valence Bond Solid (VBS) order can be realized in the 2D Heisenberg model with additional multi-spin interactions. As shown in the illustration (Figure 1), such interactions (also known as “singlet projectors”) induce valence bonds (singlets) in a crystaline pattern. When the multi-spin interaction is sufficiently strong, The candidate of the ground state of such model can be either in plaquette or columnar VBS phase. Based on quantum Monte Carlo calculation on a square lattice of relatively large size (64*64), we found the Neel–VBS transition is of second order, and this quantum phase transition complies with the Deconfined Quantum Critical Point (DQCP) theory proposed by Senthil, et. al.. Through finite size scaling analysis, we found that the transitions induced by 4-spin and 6-spin interactions are of the same universality class, as critical exponents derived are the same. This also supports the notion of DQCP. However, it is worth to mention that a very weak first order phase transition scenario can not be completely ruled out.

Figure 1

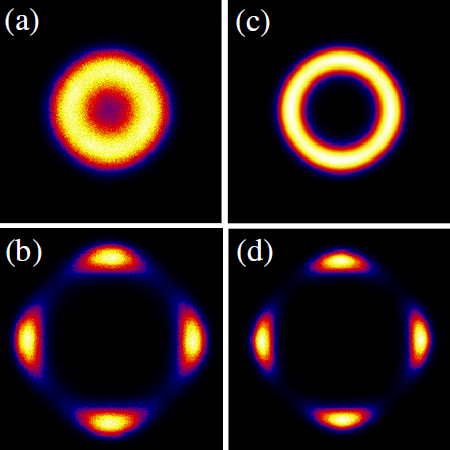
One salient feature of the DQCP theory is the emergence of U(1) symmetry near the critical point. On the other hand, the VBS phase is 4-fold symmetric spatially (Z4 symmetric). However it was not possible to study such crossover between U(1) and Z4 symmetries, due to the fact that strong VBS order can not be achieved in previous studies. In the Heisenberg model with 6-spin interactions, we are able to induce strong columnar VBS order and study such crossover (Shown in Figure 2). We also extend the symmetry of spins to SU(N). The order parameter of spatial Z4 symmetry (dimer order) is governed by a length scale Lambda which diverges faster than the spin correlation length.

Figure 2

（by Jie Lou）

Reference

  1. J. Lou, A. W. Sandvik and N. Kawashima: Antferromagnetic to valence-bond-solid transitions in two-dimensional SU(N) Heisenberg models with multi-spin interactions. Phys. Rev. B 80, 180414(R) (2009).
  2. A. W. Sandvik: Evidence for deconfined quantum criticality in a two-dimensional Heisenberg model with four-spin interactions.  Phys. Rev. Lett. 98, 227202 (2007).