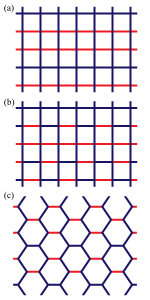
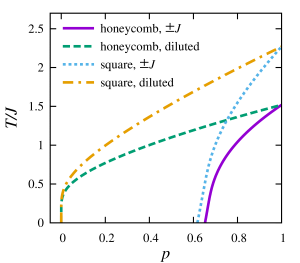
Two-dimensional Ising models on the honeycomb lattice and the square lattice with striped random impurities are studied to obtain their phase diagrams. Assuming bimodal distributions of the random impurities where all the non-zero couplings have the same magnitude, exact critical values for the fraction \(p\) of ferromagnetic bonds at the zero-temperature \(T=0\) are obtained. The critical lines in the \(p-T\) plane are drawn by numerically evaluating the Lyapunov exponent of random matrix products.