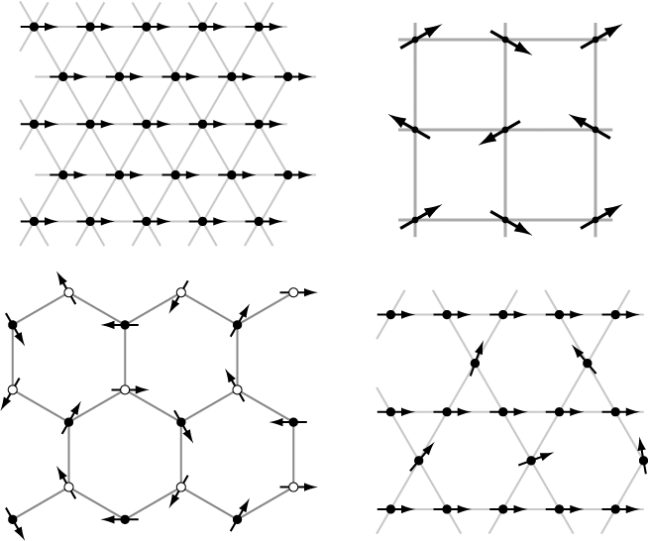
Two-dimensional Heisenberg dipolar lattices are investigated by Monte Carlo simulations. Simulations are performed on triangular, square, honeycomb, and kagome ́ lattices. Lattice-dependent magnetic structures and critical phenomena are observed. Although it is believed that two-dimensional Heisenberg dipolar lattices belong to the same universality class of two-dimensional XY dipolar lattices, results from the Monte Carlo simulations show considerable deviations in the critical exponent between the Heisenberg and XY models of triangular and square lattices. The Heisenberg dipolar honeycomb lattice exhibits unusual magnetic ordering in the form of arrays of vortices. Using finite-size scaling techniques, it is shown that the unusual order undergoes the Kosterlitz–Thouless transition. On the kagome ́ lattice, geometric frustration produces a peculiar ferromagnetic ordered state that is macroscopically degenerate. The degeneracy is expected to explain the missing magnetic entropy in ferromagnetic kagome ́, pyrochlore, and spinel substances.
(by Yusuke Tomita)