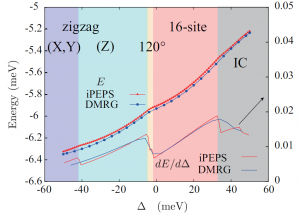
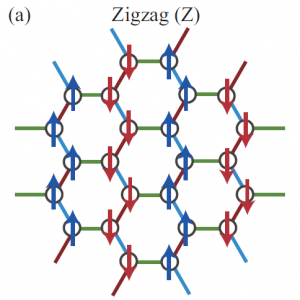
We investigate the ground state properties of Na2IrO3 based on numerical calculations of the recently proposed ab initio Hamiltonian represented by Kitaev and extended Heisenberg interactions. To overcome the limitation posed by small tractable system sizes in the exact diagonalization study employed in a previous study [Y. Yamaji et al., Phys. Rev. Lett. 113, 107201 (2014)], we apply a two-dimensional density matrix renormalization group and an infinite-size tensor-network method. By calculating at much larger system sizes, we critically test the validity of the exact diagonalization results. The results consistently indicate that the ground state of Na2IrO3 is a magnetically ordered state with zigzag configuration in agreement with experimental observations and the previous diagonalization study. Applications of the two independent methods in addition to the exact diagonalization study further uncover a consistent and rich phase diagram near the zigzag phase beyond the accessibility of the exact diagonalization. For example, in the parameter space away from the ab initio value of Na2IrO3 controlled by the trigonal distortion, we find three phases: (i) an ordered phase with the magnetic moment aligned mutually in 120 degrees orientation on every third hexagon, (ii) a magnetically ordered phase with a 16-site unit cell, and (iii) an ordered phase with presumably incommensurate periodicity of the moment. It suggests that potentially rich magnetic structures may appear in A2IrO3 compounds for A other than Na. The present results also serve to establish the accuracy of the first-principles approach in reproducing the available experimental results thereby further contributing to finding a route to realize the Kitaev spin liquid.
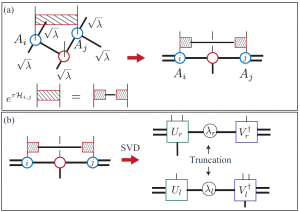
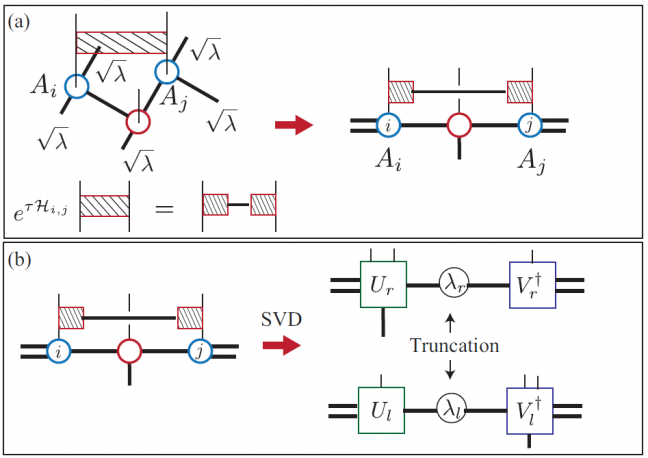
(by Naoki Kawashima)