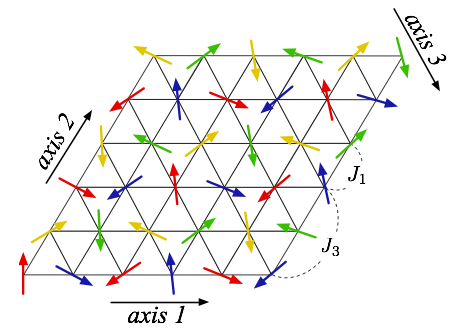
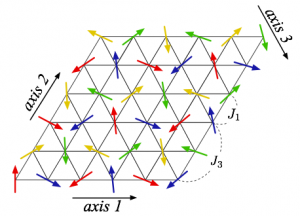
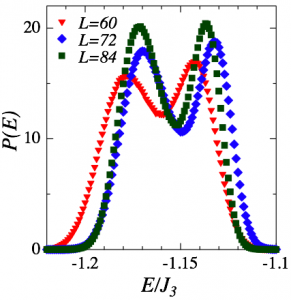
We study a finite-temperature phase transition in the two-dimensional classical Heisenberg model on a triangular lattice with a ferromagnetic nearest-neighbor interaction J1 and an antiferromagnetic third-nearest-neighbor interaction J3 using a Monte Carlo method. Apart from a trivial degeneracy corresponding to O(3) spin rotations, the ground state for J3 ≠0 has a threefold degeneracy corresponding to 120° lattice rotations. We find that this model exhibits a first-order phase transition with the breaking of the threefold symmetry when the interaction ratio is J3 / J1 = -3.
(by Ryo TAMURA)
Reference:
R. Tamura and N. Kawashima, J. Phys. Soc. Jpn. 77, 103002 (2008).