The S=1/2 Ising-like XXZ model has been intensively studied as a good stage to clarify exotic phenomena, such as supersolid behavior, stabilization of the valence-bond-solid state on frustrated lattices, and spin-flop transition in magnetic fields [1]. In particular, the spin-flop transition has been a long standing topic in condensed matter physics and the nature has been clarified by several theoretical approaches [2]; the Neel state (z-Neel) with the antiferromagnetically ordered spins along the easy-axis direction shows a first-order transition to the spin-canted state (xy-Neel) at a low temperature. An interesting point on this spin-flop transition is that the first order transition accompanying a magnetization jump occurs irrespectively of whether the quantum or the classical spins in both two-dimensional (2D) and three-dimensional (3D) isotropic lattice cases. However, in quasi-one-dimensional limit, the system can be regarded as a 1D-quantum spin chain in a low temperature region, because the interchain couplings are suppressed by the thermal fluctuation. The S=1/2 Ising-like XXZ spin chain shows a critical behavior from the transition field Hc1 up to the saturation field Hc2, when the magnetic field H is applied along the easy axis at zero temperature T=0. The low energy excitation for Hc1 < H < Hc2 is described by the Tomonaga-Luttinger (TL) liquid, which is characterized by the TL exponents appearing in the long-distance behavior of the longitudinal and transverse spin-spin correlations. An important point arising from the Ising anisotropy is that the longitudinal incommensurate correlation becomes dominant for Hc1 < H < H* while the transverse staggered one survives at long distance for H* < H < Hc2. When the interchain interactions become relevant in the TL liquid state, the long-range-ordered state corresponding to the dominant spin fluctuation can be realized, accompanying the finite-temperature phase transition. Indeed, the existence of such incommensurate order is suggested in recent experiment on a quasi 1D S=1/2 XXZ antiferromagnet BaCo2V2O8 [3].
In the above two descriptions of the field-induced transition, the phase transition in the spin-flop transition and the q1D case seem to be incompatible with each other. Then, a natural but nontrivial question may arise; Is it possible to connect the 1D-based description with the spin-flop phase diagram in the pure 2D or 3D lattice case, varying the amplitude of the interchain couplings? Since the critical phenomena are strongly affected by the dimensionality of the system, the interchain-coupling dependence of the q1D system involves some essentially important physics. The enhancement of the incommensurate fluctuation which is not hold in the classical case makes the field-induced phase of the q1D XXZ model more complicated.
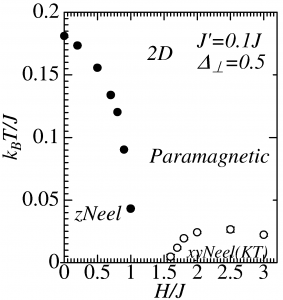
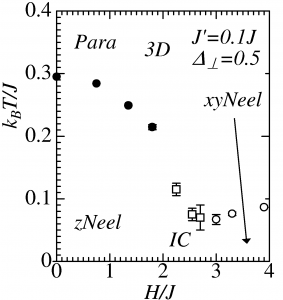
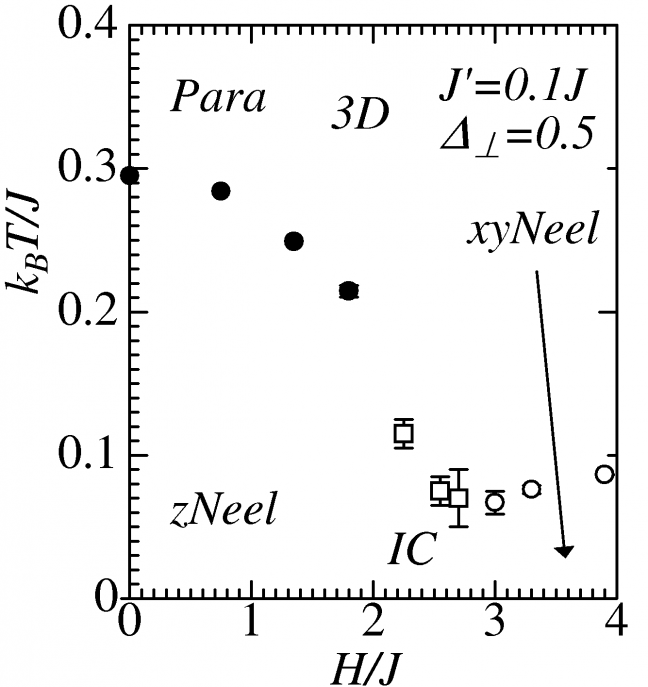
Fig.1: Phase diagrams in 2D and 3D.
We performed quantum Monte Carlo simulations based on the directed loop algorithm for the S=1/2 Ising-like XXZ spin chains constructing the 2D square lattice and 3D cubic lattice through weak interchain couplings. Based on the obtained results, we illustrated the H-T phase diagrams in Figure 1. In the low magnetized region of the 2D case, there is no finite temperature transition because incommensurate correlations along both the spin-chain and the interchain directions suppress the development of a two-dimensional antiferromagnetic correlation. On the other hand, in the 3D case, the incommensurate fluctuation can be stabilized as a long-range-ordered state at a finite temperature [4].
(by Takafumi Suzuki)
References
[1] F. H’ebert, et al., Phys. Rev. B 65, 014513 (2001); M. Boninsegni and N. Proko’ev, Phys. Rev. Lett. 95, 237204 (2005); D. C. Cabra, et al., Phys. Rev. B 71, 144420 (2005); S. V. Isakov, et al., Phys. Rev. Lett. 97, 147202 (2005); A. Banerjee, et al., Phys. Rev. Lett. 100, 047208 (2008).[2] A. van Otterlo, et al., Phys. Rev. B 52, 16176 (1995); M. Kohno and M. Takahashi, Phys. Rev. B 56, 3212 (1997); G. Schmid, et al., Phys. Rev. Lett. 88, 167208 (2005).
[3] S. Kimura, et al., Phys. Rev. Lett. 99, 087602 (2007).
[4] T. Suzuki and N. Kawashima, K. Okunishi, J. Phys. Soc. Jpn. 76, 123707 (2007); K. Okunishi and T. Suzuki, Phys. Rev. B 76, 224411 (2007).