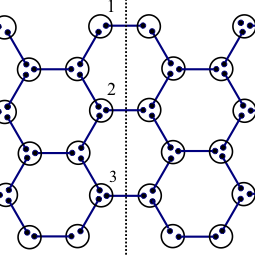
We study quantum entanglement in the ground state of the Affleck-Kennedy-Lieb-Tasaki (AKLT) model defined on two-dimensional graphs with reflection and/or inversion symmetry. The ground state of this spin model is known as the valence-bond-solid state. We investigate the properties of reduced density matrix of a subsystem which is a mirror image of the other one. Thanks to the reflection symmetry, the eigenvalues of the reduced density matrix can be obtained by numerically diagonalizing a real symmetric matrix whose elements are calculated by Monte Carlo integration. We calculate the von Neumann entropy of the reduced density matrix. The obtained results indicate that there is some deviation from the naive expectation that the von Neumann entropy per valence bond on the boundary between the subsystems is ln2. This deviation is interpreted in terms of the hidden spin chain along the boundary between the subsystems. In some cases where graphs are on ladders, the numerical results are analytically or algebraically confirmed.
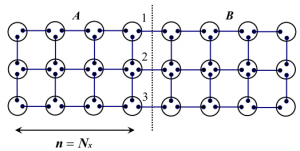
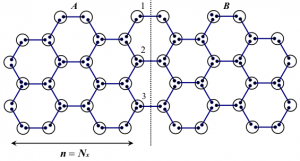
(by Shu Tanaka)
Reference
[1] Hosho Katsura, Naoki Kawashima, Anatol N. Kirillov, Vladimir E. Korepin and Shu Tanaka, J. Phys. A: Math. Theor. 43 (2010) 255303.