The ordinary Heisenberg model that possesses the SU(2) symmetry can easily be generalized to higher symmetry simply by regarding a symbol “S” in the Heisenberg Hamiltonian as a generator of the SU(N) algebra rather than SU(2). This very simple and fundamental model, according to some theoretical predictions, exhibits surprizingly wide variety of ground states depending upon the value of N and the representation, in two dimensions. Here, chaging the representation corresponds to changing the magnitude of spins in the ordinary SU(2) Heisenberg model. While the representation-dependent ground state is well-known as a Haldane phenomenon in one dimension, no systematic numerical study has been done in two dimensions. We employed quantum Monte Carlo method to study this model system, using newly-developed algorithm. We found that the ground state is the Neel state for N is 4 or smaller, whereas for N larger than 4 the lattice translational symmetry is broken to yield a dimerized state as shown schematically in Fig.1. (Darker lines correspond to pairs of nearest-neighbor spins with larger correlation.)

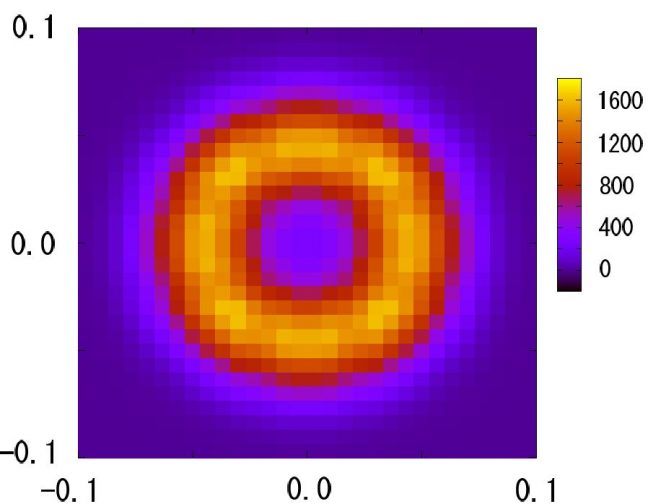
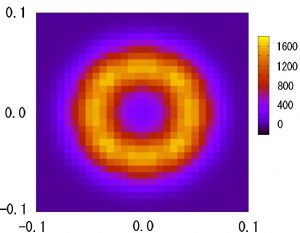
Moreover, the space of the ground states has an approximate U(1) symmetry. Figure 2 shows the distribution function of the dimer order parameters in the x and the y directions. In the case of larger representations, we observed that non-trivial spontaneous spatial structure is suppressed.
(by Naoki KAWASHIMA)
References
- Kenji Harada, Naoki Kawashima and Matthias Troyer: “Neel and Spin-Peierls ground states of two-dimensional SU(N) quantum antiferromagnets”, Phys. Rev. Lett. 90 117203-117206 (2003).
- Naoki Kawashima and Yuta Tanabe: “Representation-Dependent Ground-States of the SU(N) Heisenberg Model”, Phys. Rev. Lett. 98 057202(1-4) (2007).