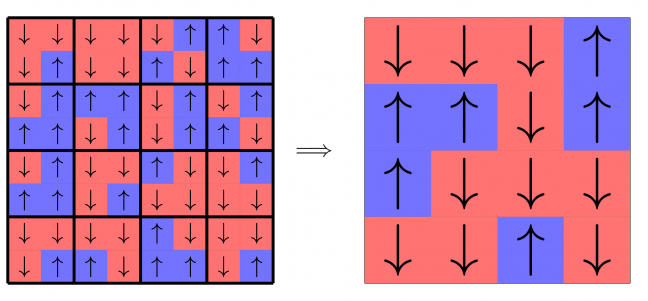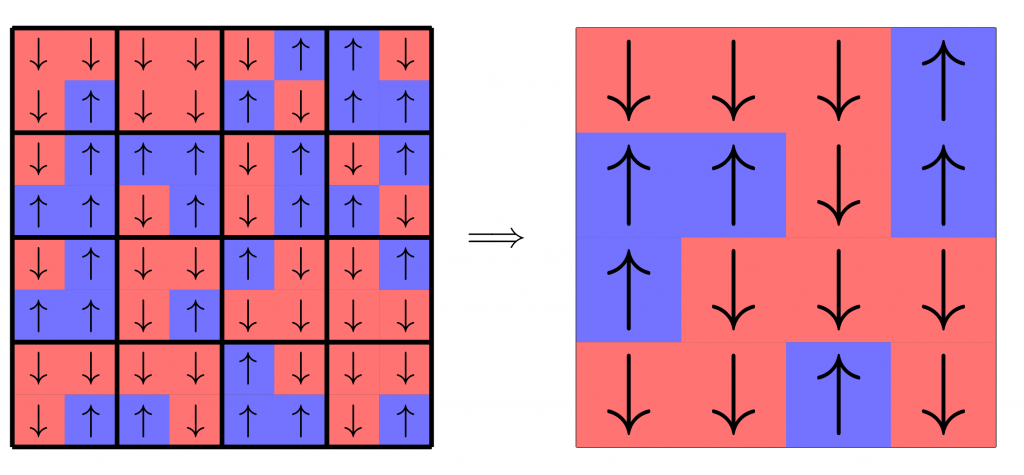
Block-spin transformations (Fig. 1) are a simple way to implement the real-space renormalization group (RSRG) for spin models. They work by dividing the lattice into blocks and determining representative spins for each block according to some rule or map. Two common choices of these maps are decimation, where the spin at a particular site is always chosen to represent the block, and the majority rule, where the most frequent spin in a block is chosen to represent it. By repeatedly applying each of these two maps to a large critical configuration, we can see that there is a qualitative difference in their effect (Fig. 2). Decimation is relatively well-understood, as it can be treated analytically, but despite the popularity and accessibility of the majority rule map, its behavior has not been thoroughly studied analytically or even numerically.

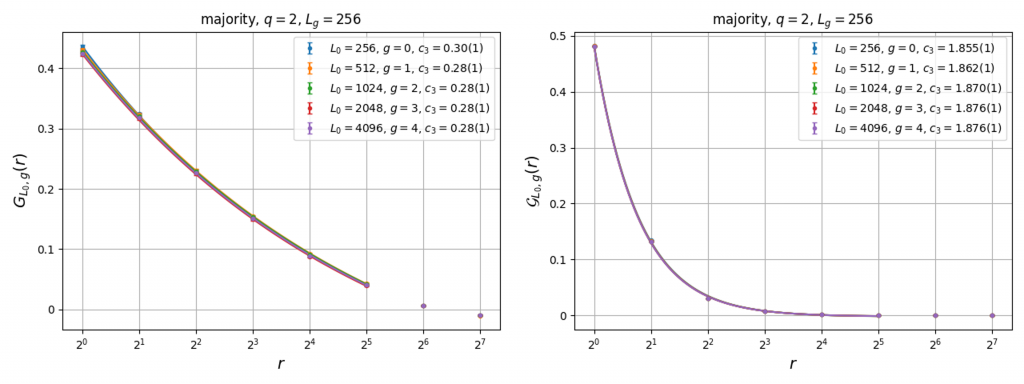
In our paper [1], we obtained numerical data to answer the question of whether the majority rule map brings us to the correct fixed point. We simulated large critical \(q=2,3,4\) Potts model configurations and repeatedly applied \(2\times2\) RSRG map iterations to the configurations to examine the spin and energy correlation functions across different choices of the RSRG map, including the decimation map and the majority rule map. We found that when the renormalized lattice size \(L_g\) is fixed, allowing the initial lattice size \(L_0\) and number of iterations \(g\) to vary, the RG flow of the aforementioned correlation functions converge to a nontrivial curve with the correct scaling behavior, under the majority rule map on critical Potts configurations (Fig. 3). We denote this property as “faithfulness”, as the RSRG map correctly preserves the critical behavior of the model under repeated iteration. We also provided an explanation for why the majority rule correctly reproduces the scaling of the magnetization in [1].
References
- K. O. Akamatsu and N. Kawashima, J. Stat. Phys. 191, 109 (2024).