Author: Ryui Kaneko

Several quantum magnets comprise two sublattices of magnetic ions coupled by a geometrically frustrated exchange. This is for instance the case of a Heisenberg antiferromagnet on a body centered tetragonal lattice or a square lattice with nearest- and next-nearest-neighbor exchange interactions. In the regime of intersublattice coupling smaller than the intrasublattice exchange, it can be shown that the frustrated nature of the intersublattice exchange precludes a bilinear coupling between the order parameters of the two sublattices. The Hamiltonian symmetry only allows for an effective biquadratic coupling. The biquadratic interaction tends to align the order parameters of the sublattices in either parallel or antiparallel. This results in the Ising-like Z2 symmetry breaking in the ground state in addition to the usual spin-rotational symmetry breaking.

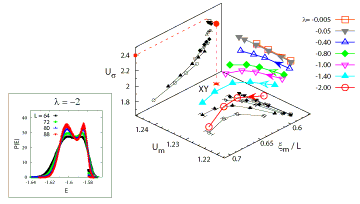
In Ref. 1, we investigated such a phase transition with the additional Ising-like symmetry breaking for the XY spin case, which is relevant for a spin-dimer compound BaCuSi2O6 [1]. More specifically, we performed Monte Carlo simulations to obtain a renormalization group flow diagram around the decoupled model with intersublattice interaction (∝ λ) being zero. Figure 1 is the obtained flow diagram. It shows several parameters of zero scaling dimensions and therefore at second order transitions the flow should converge to a stable fixed point. It can be clearly seen that the flow starting around the decoupled XY fixed point (indicated by a large filled circle) systematically deviates from it, evolving toward the region where a clear first order signature is obtained (λ = -2; see the inset where an energy histogram with the double-peak structure is shown).

Neither a separatrix nor a stable fixed point is found. It means that the biquadratic coupling is relevant at the decoupled XY fixed point (this can also be shown using a scaling argument [2]), and the resulting crossover behavior leads to a first-order transition.

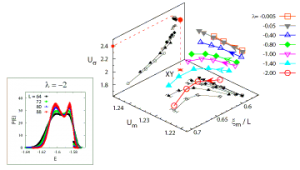
So far there is no experimental report suggesting the first-order transition in BaCuSi2O6, and the experimental data such as specific heat can be fitted using the XY model. The reason is that BaCuSi2O6 is a quasi-two-dimensional system and thus the intersublattice biquadratic coupling which arises from second-order perturbation with respect to the ratio between the interlayer and the intralayer bilinear exchange coupling is extremely small in this case. Namely, the true discontinuous nature of the transition can be observed in a very narrow region near the transition point that could be easily beyond the standard experimental precision.

(by Yoshitomo Kamiya)

References

[1] Y. Kamiya, N. Kawashima, and C. D. Batista, J. Phys. Soc. Jpn. 78, 094008 (2009).
[2] Y. Kamiya, N. Kawashima, and C. D. Batista, Phys. Rev. B 82, 054426 (2010).

The S=1/2 Ising-like XXZ model has been intensively studied as a good stage to clarify exotic phenomena, such as supersolid behavior, stabilization of the valence-bond-solid state on frustrated lattices, and spin-flop transition in magnetic fields [1]. In particular, the spin-flop transition has been a long standing topic in condensed matter physics and the nature has been clarified by several theoretical approaches [2]; the Neel state (z-Neel) with the antiferromagnetically ordered spins along the easy-axis direction shows a first-order transition to the spin-canted state (xy-Neel) at a low temperature. An interesting point on this spin-flop transition is that the first order transition accompanying a magnetization jump occurs irrespectively of whether the quantum or the classical spins in both two-dimensional (2D) and three-dimensional (3D) isotropic lattice cases. However, in quasi-one-dimensional limit, the system can be regarded as a 1D-quantum spin chain in a low temperature region, because the interchain couplings are suppressed by the thermal fluctuation. The S=1/2 Ising-like XXZ spin chain shows a critical behavior from the transition field Hc1 up to the saturation field Hc2, when the magnetic field H is applied along the easy axis at zero temperature T=0. The low energy excitation for Hc1 < H < Hc2 is described by the Tomonaga-Luttinger (TL) liquid, which is characterized by the TL exponents appearing in the long-distance behavior of the longitudinal and transverse spin-spin correlations. An important point arising from the Ising anisotropy is that the longitudinal incommensurate correlation becomes dominant for Hc1 < H < H* while the transverse staggered one survives at long distance for H* < H < Hc2. When the interchain interactions become relevant in the TL liquid state, the long-range-ordered state corresponding to the dominant spin fluctuation can be realized, accompanying the finite-temperature phase transition. Indeed, the existence of such incommensurate order is suggested in recent experiment on a quasi 1D S=1/2 XXZ antiferromagnet BaCo2V2O8 [3].

In the above two descriptions of the field-induced transition, the phase transition in the spin-flop transition and the q1D case seem to be incompatible with each other. Then, a natural but nontrivial question may arise; Is it possible to connect the 1D-based description with the spin-flop phase diagram in the pure 2D or 3D lattice case, varying the amplitude of the interchain couplings? Since the critical phenomena are strongly affected by the dimensionality of the system, the interchain-coupling dependence of the q1D system involves some essentially important physics. The enhancement of the incommensurate fluctuation which is not hold in the classical case makes the field-induced phase of the q1D XXZ model more complicated.

We performed quantum Monte Carlo simulations based on the directed loop algorithm for the S=1/2 Ising-like XXZ spin chains constructing the 2D square lattice and 3D cubic lattice through weak interchain couplings. Based on the obtained results, we illustrated the H-T phase diagrams in Figure 1. In the low magnetized region of the 2D case, there is no finite temperature transition because incommensurate correlations along both the spin-chain and the interchain directions suppress the development of a two-dimensional antiferromagnetic correlation. On the other hand, in the 3D case, the incommensurate fluctuation can be stabilized as a long-range-ordered state at a finite temperature [4].

(by Takafumi Suzuki)

References

[1] F. H’ebert, et al., Phys. Rev. B 65, 014513 (2001); M. Boninsegni and N. Proko’ev, Phys. Rev. Lett. 95, 237204 (2005); D. C. Cabra, et al., Phys. Rev. B 71, 144420 (2005); S. V. Isakov, et al., Phys. Rev. Lett. 97, 147202 (2005); A. Banerjee, et al., Phys. Rev. Lett. 100, 047208 (2008).
[2] A. van Otterlo, et al., Phys. Rev. B 52, 16176 (1995); M. Kohno and M. Takahashi, Phys. Rev. B 56, 3212 (1997); G. Schmid, et al., Phys. Rev. Lett. 88, 167208 (2005).
[3] S. Kimura, et al., Phys. Rev. Lett. 99, 087602 (2007).
[4] T. Suzuki and N. Kawashima, K. Okunishi, J. Phys. Soc. Jpn. 76, 123707 (2007); K. Okunishi and T. Suzuki, Phys. Rev. B 76, 224411 (2007).