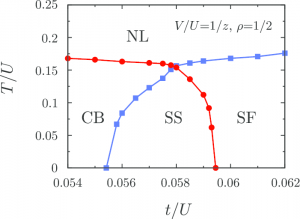
Using an unbiased quantum Monte Carlo method, we obtain convincing evidence of the existence of a checkerboard supersolid at a commensurate filling factor \(1/2\) (a commensurate supersolid) in the soft-core Bose-Hubbard model with nearest-neighbor repulsions on a cubic lattice. In conventional cases, supersolids are realized at incommensurate filling factors by a doped-defect-condensation mechanism, where particles (holes) doped into a perfect crystal act as interstitials (vacancies) and delocalize in the crystal order. However, in the model, a supersolid state is stabilized even at the commensurate filling factor \(1/2\) without doping. By performing grand canonical simulations, we obtain a ground-state phase diagram that suggests the existence of a supersolid at a commensurate filling. To obtain direct evidence of the commensurate supersolid, we next perform simulations in canonical ensembles at a particle density \(\rho = 1/2\) and exclude the possibility of phase separation. From the obtained snapshots, we discuss its microscopic structure and observe that interstitial-vacancy pairs are unbound in the crystal order. (Abstract of Ref.[2])

(by T. Ohgoe)
Reference
[1] A. F. Andreev and I. M. Lifshitz, Sov. Phys. JETP 29, 1107 (1969).[2] T. Ohgoe, T. Suzuki, and N. Kawashima, Phys. Rev. Lett. 108, 185302 (2012).
[3] T. Ohgoe, T. Suzuki, and N. Kawashima, Phys. Rev. B 86, 054520 (2012).
