


The Institute for Solid State Physics, The University of Tokyo




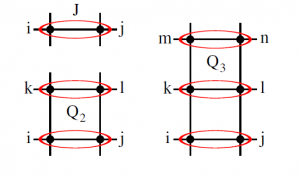
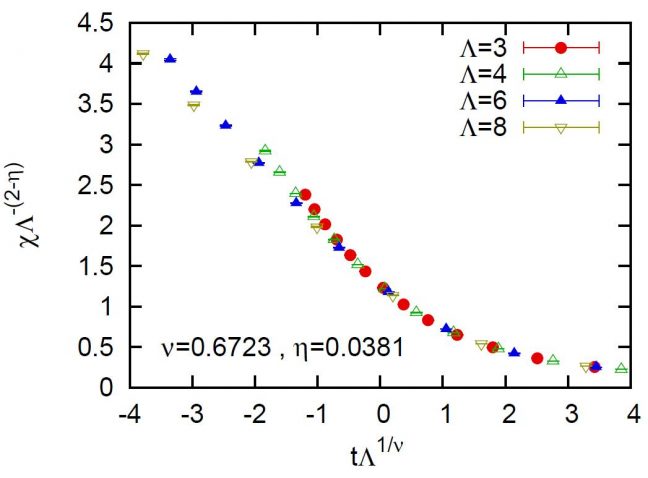
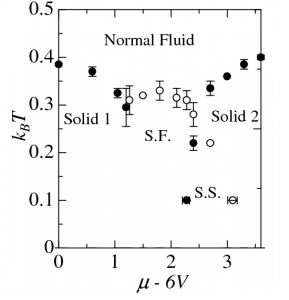
The quantum phase transition from the Neel order to the Valence Bond Solid (VBS) order can be realized in the 2D Heisenberg model with additional multi-spin interactions. As shown in the illustration (Figure 1), such interactions (also known as “singlet projectors”) induce valence bonds (singlets) in a crystaline pattern. When the multi-spin interaction is sufficiently strong, The candidate of the ground state of such model can be either in plaquette or columnar VBS phase. Based on quantum Monte Carlo calculation on a square lattice of relatively large size (64*64), we found the Neel–VBS transition is of second order, and this quantum phase transition complies with the Deconfined Quantum Critical Point (DQCP) theory proposed by Senthil, et. al.. Through finite size scaling analysis, we found that the transitions induced by 4-spin and 6-spin interactions are of the same universality class, as critical exponents derived are the same. This also supports the notion of DQCP. However, it is worth to mention that a very weak first order phase transition scenario can not be completely ruled out.
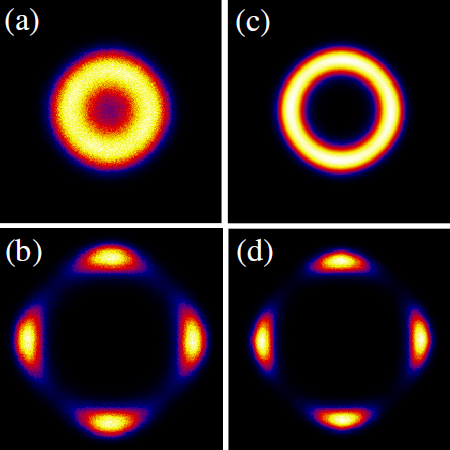
One salient feature of the DQCP theory is the emergence of U(1) symmetry near the critical point. On the other hand, the VBS phase is 4-fold symmetric spatially (Z4 symmetric). However it was not possible to study such crossover between U(1) and Z4 symmetries, due to the fact that strong VBS order can not be achieved in previous studies. In the Heisenberg model with 6-spin interactions, we are able to induce strong columnar VBS order and study such crossover (Shown in Figure 2). We also extend the symmetry of spins to SU(N). The order parameter of spatial Z4 symmetry (dimer order) is governed by a length scale Lambda which diverges faster than the spin correlation length.
(by Jie Lou)
We consider a classical XY-like Hamiltonian on a body-centered tetragonal lattice, focusing on the role of interlayer frustration. A three-dimensional (3D) ordered phase is realized via thermal fluctuations, breaking the mirror-image reflection symmetry in addition to the XY symmetry. A heuristic field-theoretical model of the transition has a decoupled fixed point in the 3D XY universality, and our Monte Carlo simulation suggests that there is such a temperature region where long-wavelength fluctuations can be described by this fixed point. However, it is shown using scaling arguments that the decoupled fixed point is unstable against a fluctuation-induced biquadratic interaction, indicating that a crossover to nontrivial critical phenomena with different exponents appears as one approaches the critical point beyond the transient temperature region. This new scenario clearly contradicts the previous notion of the 3D XY universality.
(by Yoshitomo Kamiya)
Y. K., Naoki Kawashima, and Cristian D. Batista: “Finite-Temperature Transition in the Spin-Dimer Antiferromagnet BaCuSi2O6,” J. Phys. Soc. Jpn. 78 (2009) 094008
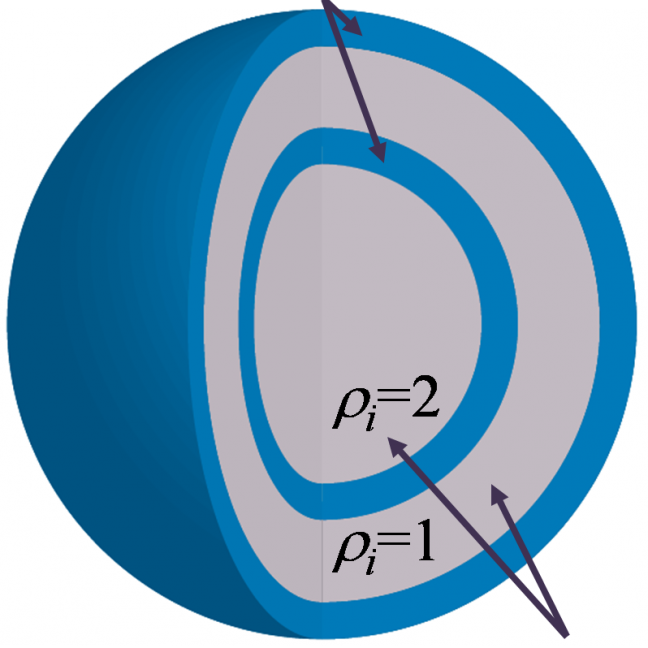
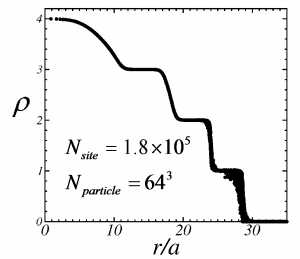
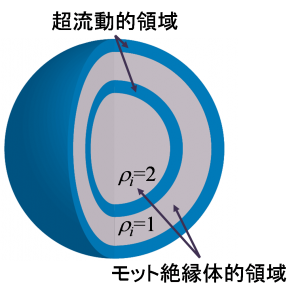
We study the Bose-Hubbard model with an external harmonic field, which is effective for modeling a cold atomic Bose gas trapped in an optical lattice. We modify the directed-loop algorithm to simulate large systems efficiently. As a demonstration we carry out the simulation of a system consisting of 1.8×105 particles on a 643 lattice. These numbers are comparable to those in the pioneering experimental work by Greiner et al. [Nature (London) 415, 39 (2002)]. Furthermore, we observe coherence between two superfluid spheres separated by a Mott insulator region in a “wedding-cake” structure.
(by Yasuyuki Kato)
Yasuyuki Kato and Naoki Kawashima, “Quantum Monte Carlo method for the Bose-Hubbard model with harmonic confining potential” Phys. Rev. E. 79, 021104 (2009).
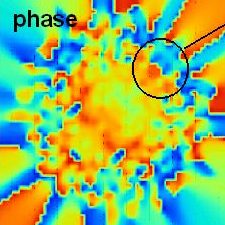
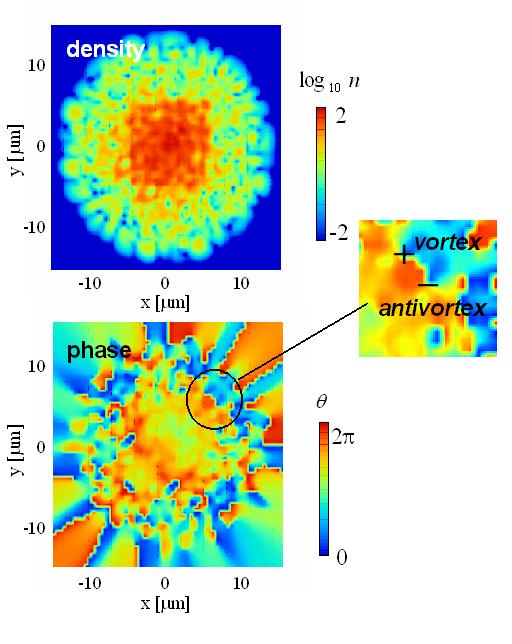
We study the finite-temperature transition of the quasi-2D Bose gas in an uniaxially-compressed harmonic trap by numerically solving the projected Gross-Pitaevskii equation. Gradual emergence of superfluidity is confirmed by calculating the moment of inertia when a temperature decreases. By investigating the long-distance behavior of a phase correlation function, superfluid density gradually increases reflecting the development of the phase correlation around the center of the system. From these results, we obtain the evidence for the emergence of superfluidity in this system directly.
Toshihiro Sato, Takafumi Suzuki and Naoki Kawashima, J. Phys.: Conf. Ser. 150, 032094 (2009)



We modify the directed-loop algorithm (DLA) to solve the problem that typically arises from large on-site interaction. The large on-site interaction is inevitable when one tries to simulate a Bose gas system in continuum by discretizing the space with small lattice spacings. While the efficiency of a straightforward application of DLA decreases as the mesh becomes finer, the performance of the new method does not depend on it except for the trivial factor due to the increase in the number of lattice points.
(Abstract of Ref. [1])
(By Yasuyuki Kato)
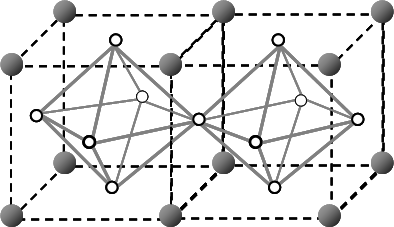
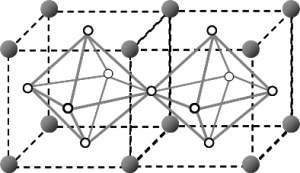
We investigate a supersolid state in hardcore boson models on the face-centered-cubic (fcc) lattice. The supersolid state is characterized by a coexistence of crystalline order and superfluidity. Using a quantum Monte Carlo method based on the directed-loop algorithm, we calculate static structure factors and superfluid density at finite temperature, from which we obtain the phase diagram. The supersolid phase exists at intermediate fillings between a three-quarter-filled solid phase and a half-filled solid phase. We also discuss the mechanism of the supersolid state on the fcc lattice.
(Abstract of Ref. [1])
(by Takafumi Suzuki)
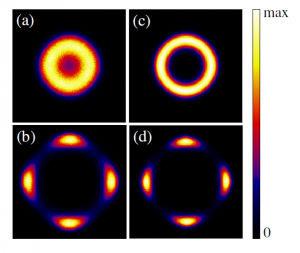
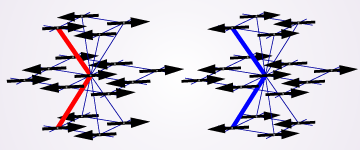
The ordinary Heisenberg model that possesses the SU(2) symmetry can easily be generalized to higher symmetry simply by regarding a symbol “S” in the Heisenberg Hamiltonian as a generator of the SU(N) algebra rather than SU(2). This very simple and fundamental model, according to some theoretical predictions, exhibits surprizingly wide variety of ground states depending upon the value of N and the representation, in two dimensions. Here, chaging the representation corresponds to changing the magnitude of spins in the ordinary SU(2) Heisenberg model. While the representation-dependent ground state is well-known as a Haldane phenomenon in one dimension, no systematic numerical study has been done in two dimensions. We employed quantum Monte Carlo method to study this model system, using newly-developed algorithm. We found that the ground state is the Neel state for N is 4 or smaller, whereas for N larger than 4 the lattice translational symmetry is broken to yield a dimerized state as shown schematically in Fig.1. (Darker lines correspond to pairs of nearest-neighbor spins with larger correlation.)

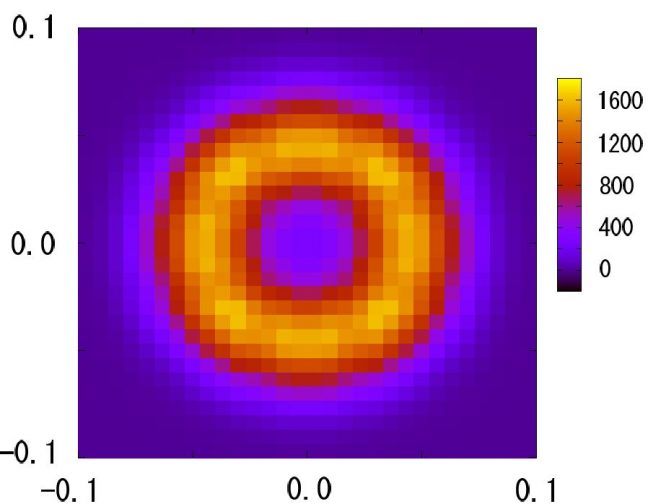
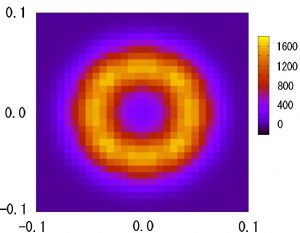
Moreover, the space of the ground states has an approximate U(1) symmetry. Figure 2 shows the distribution function of the dimer order parameters in the x and the y directions. In the case of larger representations, we observed that non-trivial spontaneous spatial structure is suppressed.
(by Naoki KAWASHIMA)
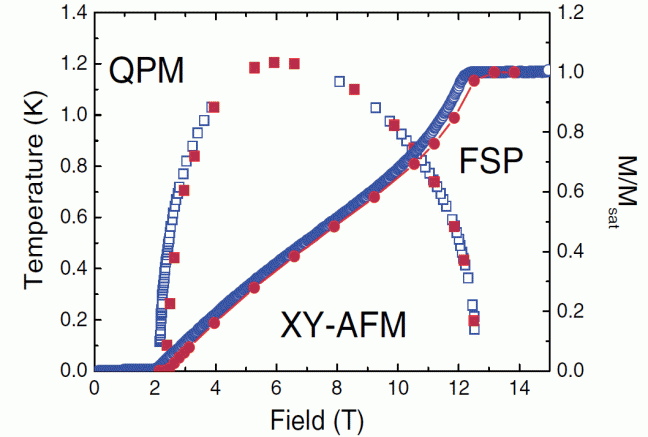
NiCl2−4SC(NH2)2 (DTN) is a quantum S=1 chain system with strong easy-pane anisotropy and a new candidate for the Bose-Einstein condensation of the spin degrees of freedom. ESR studies of magnetic excitations in DTN in fields up to 25 T are presented. Based on analysis of the single-magnon excitation mode in the high-field spin-polarized phase and previous experimental results [Phys. Rev. Lett. 96, 077204 (2006)], a revised set of spin-Hamiltonian parameters is obtained. Our results yield D=8.9 K, Jc=2.2 K, and Ja,b=0.18 K for the anisotropy, intrachain, and interchain exchange interactions, respectively. These values are used to calculate the antiferromagnetic phase boundary, magnetization, and the frequency-field dependence of two-magnon bound-state excitations predicted by theory and observed in DTN for the first time. Excellent quantitative agreement with experimental data is obtained. (Abstract of Ref. [1])

(by Mitsuaki Tsukamoto)