The Institute for Solid State Physics, The University of Tokyo



A press release has been issued on a joint research project with Kenji Harada of Kyoto University and Tsuyoshi Okubo of the Department of Physics at the University of Tokyo, entitled “Generative model using tensor networks: Emergence of correlation structure from stock price fluctuation patterns.”
https://www.issp.u-tokyo.ac.jp/maincontents/news2.html?pid=26866

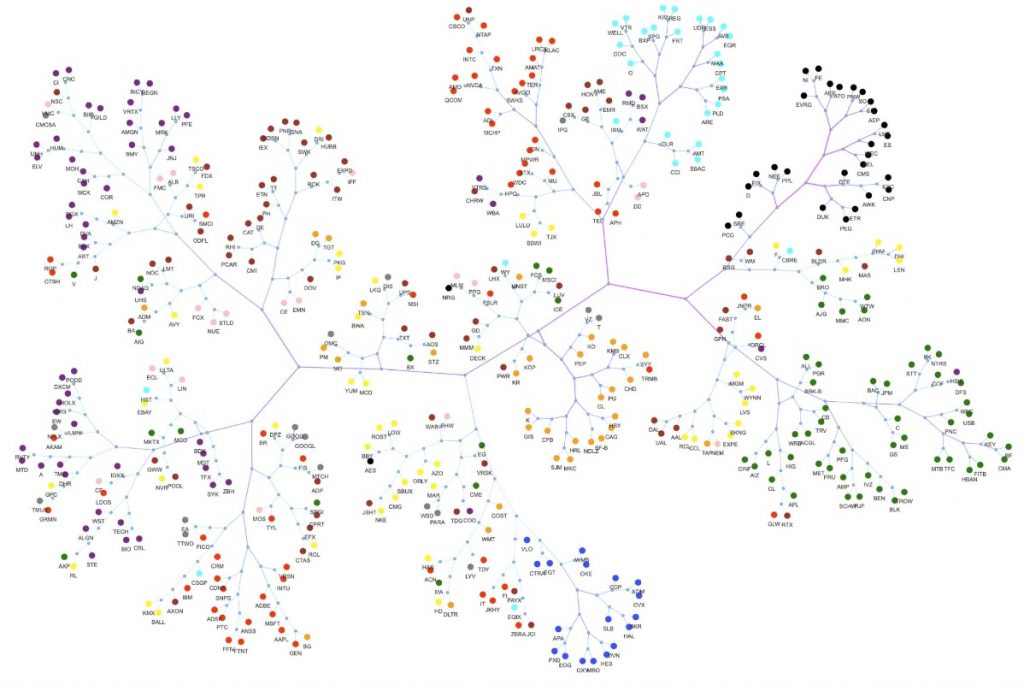
We proposed [1] a new method for constructing a generative model based on a tensor network (TN) and demonstrated its effectiveness. In most cases, generative models are based on neural networks, and optimization of the network structure has not been fully investigated. We considered a Born machine that uses the correspondence between wave functions expressed as TNs and probability distributions represented as their amplitude. Based on this correspondence, we proposed a generative model construction method (adaptive tensor tree, ATT) that optimizes the network structure, and demonstrated its effectiveness. The structure optimization was performed to minimize the mutual information carried by the tree branches. In other words, if the mutual information of each branch decreases when the surrounding branches are rearranged, the rearrangement is performed. As an example, when a generative model was constructed using ATT from data on stock price rise and fall patterns, it was observed that the correlation between stocks was naturally reflected in the network structure as learning progressed. The figure shows a tree structure generated by a Born machine based on an adaptive tensor tree (ATT) learning about 10 years of rise and fall patterns of the S&P 500. Each dot represents a company, and the color changes depending on the industry category (called “sector”). Although sector information was not provided as learning information for ATT, it can be seen that it has “discovered” that there is a close relationship between the sector and the branch structure. Because ATT can build a generative model for any sample, it is expected to be useful for elucidating various correlation structures that were previously difficult to capture, and may provide a new framework for building AI.
(https://doi.org/10.1088/2632-2153/adc2c7)
We considered a Bose-Hubbard model on a two-dimensional lattice. We showed that the model parameters (the lattice structure, the hopping constants, and the chemical potential) can be tuned in such a way that the ground state is generated by applying, to the vacuum, N creation operators of locally-defined quasi-particles, where N is proportional to the total number of lattice points. The resulting model has a free parameter β that controls the degree of quantum fluctuation; β=0 for no fluctuation and β=1/2 for the maximum fluctuation. We carried out Monte Carlo simulation of this model at zero temperature, and discovered that the model undergoes a quantum phase transition when we change this parameter. While the system is 2+1 dimensional, the new phase transition exhibits the characteristics of 2 dimensions, i.e., the Kosterlitz-Thouless phase transition analogous to the classical XY model in 2 dimensions. Accordingly, the large β phase is the quasi Bose-Einstein condensation phase.
The above-mentioned ground state is expressed exactly as a tensor network with the bond dimension 2. Tracing out this tensor network is equivalent to calculating the partition function of some classical loop gas model. This is why the quantum criticality exhibits the purely 2-dimensional characteristics. It also allows us to construct a Monte Carlo algorithm for efficient sampling from the space of classical occupation-number configurations. In other words, we can stochastically trace out the tensor network to obtain various physical quantities of interest, such as the static structure factors and the helicity modulus.

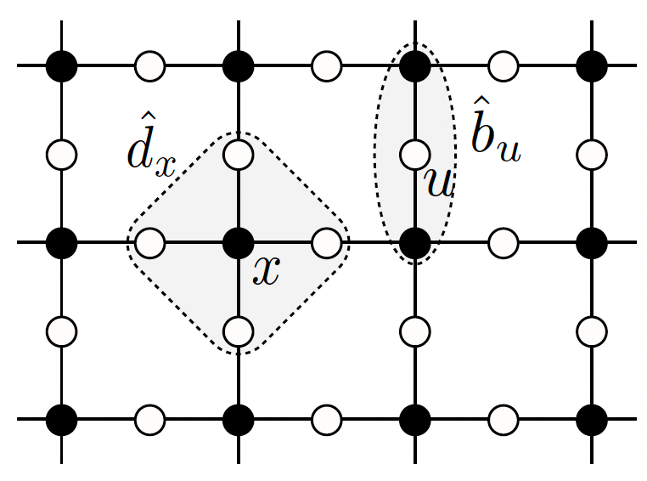
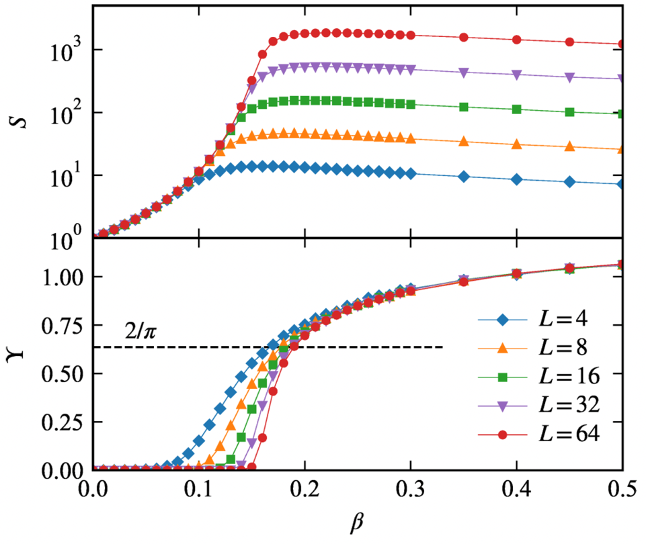
The lattice is generated from the square lattice by duplicating each bond into p copies and introducing an additional site in the middle of each copy. (Fig. 1) The direct hopping is allowed only within local clusters labelled by either x or u. While bosons interact with each other, the model is constructed in such a way that the dispersion of a single particle has a flat band if influence of the other paricles could be neglected. The result of the Monte Carlo simulation are shown in Fig.2. The static structure factor diverges around β=0.2 and, at the same time, the helicity modulus jumps from 0 to 2/π, the universal value characteristic to the KT transition.

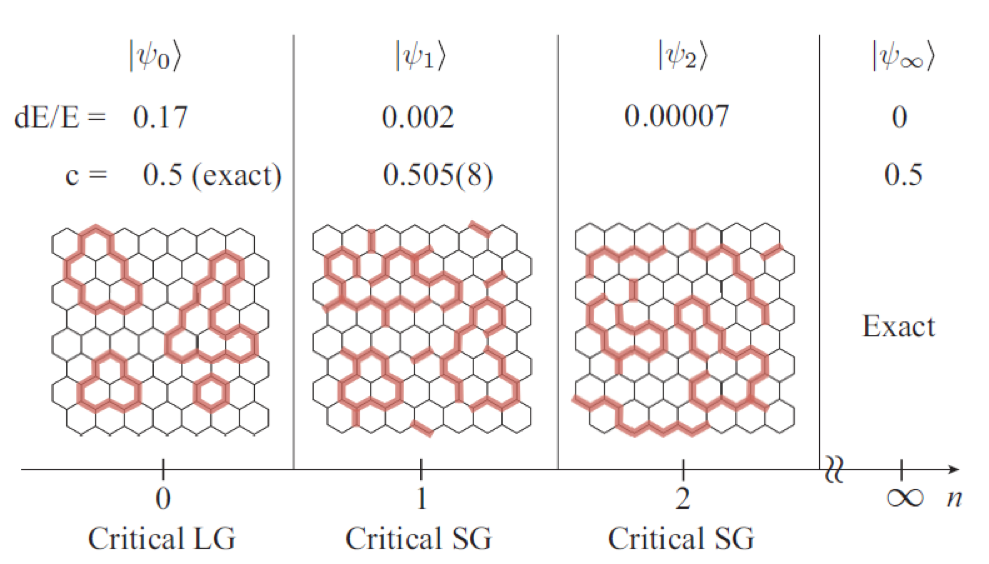
Quantum spin liquids (QSLs) represent a state of quantum matter which is not characterized by any local order parameters even at zero temperature. These novel states are expected to exhibit non-trivial entanglement structure leading to the topological order and fractionalized excitations. For example, the Haldane phase, which is known as a symmetry-protected topological phase, is a fascinating phase one can find in the S=1 quantum spin chain. The novel character that discriminates the Haldane phase from trivial gapped states was clearly revealed by the discovery of Affleck-Kennedy-Lieb-Tasaki (AKLT) model and its exact ground state known as the AKLT state. Its compact representation in the form of a matrix-product state provided a new insight into the Haldane phase. As a two-dimensional system with spin-liquid state, the Kitaev model on honeycomb lattice (KHM) is now a subject of active research, due to recent successful realizations of Kitaev materials. The model is exactly solvable and exhibits gapless and gapped Kitaev spin liquid (KSL) ground states with fractionalized excitations. One may naturally wonder if there is a simple tensor-network representation that captures the essence of the KSL, i.e., a 2D analogue of the correspondence between the AKLT state and the Haldane state.
In this work, we propose a “loop-gas” state, i.e., an exactly-solvable quantum state that has a compact and exact tensor-network representation, as well as a series of ansatze that starts from the loop-gas state and converges rapidly to the KHM ground-state. The loop gas state is defined by the loop-gas projector applied to a product state in which all spins are aligned in the (111) direction. The loop-gas projector is defined as tensor-network operator with bond-dimension 2. Specifically, it is expressed as a sum of all loop configurations, each corresponding to a product of Pauli operators on all lattice points. (Fig.1) We find that the norm of the loop gas state has exactly the same as the classical loop gas model at the critical fugacity on honeycomb lattice. The classical loop gas model appears in the low-temperature expansion of the Ising model, and therefore shares the same critical properties as the latter. These observations establishes that the correlation function of the loop-gas state is exactly the same as the correlation function of the critical Ising model. Furthermore, by defining the dimer-gas operator in an analogous way to the loop-gas operator, and applying it to the loop-gas state, we can improve the loop-gas state as an approximate to the KHM ground-state. (Fig.2) For example, the second order approximation, which is obtained by applying the dimer-gas operator twice, achieves more than 4-digits accuracy in the energy, which is better than any other previous variational wave function. Also, note that there are only two adjustable parameters in the ansatz.
From these results, we conclude that the series of ansatze starting from the loop-gas state correctly reflects the essential properties of the family of KSLs, which is known to belong to the Ising universality class. Since the present description of KSLs does not rely on the mapping to fermions, it may provide us with an alternative view point for studying KSLs.
References
[1] Hyun-Yong Lee, Ryui Kaneko, Tsuyoshi Okubo and Naoki Kawashima: Phys. Rev. Lett. 123, 087203 (2019) (arXiv:1901.05786).