It is widely known that there is no spontaneous symmetry breaking in 1d classical systems at finite temperature, which suggests that 1d classical many body problems are almost trivial and boring.
Then, let us consider 1d classical `edges’ in 2d systems, or 1d classical systems attached to a 2d bulk.
Does something interesting happen in these 1d edges?
In fact, the situation is a bit different from the simple 1d cases.
When the 2d bulk is at criticality, in particular, the strong correlation at the bulk helps the edge ordering, which results in a variety of phase transitions on the 1d edges.
For example, the 2d classical tricritical Ising model exhibits a finite-surface-temperature symmetry breaking on its 1d edge, when the bulk is fine-tuned at the tricritical point [1].
It is also known that another surface transition occurs driven by the surface external fields.
As a theoretical way of studying surface criticality, boundary conformal field theory (BCFT) is very powerful, particularly for 2d classical / 1+1d quantum systems at criticality.
It could be essential to understand surface critical behavior precisely, since the restriction of the conformal invariance may enable us not only to classify the conformal boundary conditions but also to investigate stability of boundary fixed points and exact values of scaling dimensions.
Now, let us consider an extension of the above classical tricritical Ising model in 2d, called the tricritical 3-state Potts model, whose symmetry of the spin is \(S_3\) rather than \(Z_2\).
The Monte Carlo simulation of this model suggests, similarly to the tricritical Ising, rich surface phase transitions when the bulk is at tricriticality [2].
However, the precise study from the view point of BCFT has been missing for a long time.
In order to investigate the more detailed surface phase diagram of this model, we utilize the \(ADE\) classification of the minimal-series BCFTs and perform numerical simulation with tensor network renormaization (TNR) [3,4,5].
The tricritical 3-state Potts model can be described by the \(D\)-type minimal CFT with \(c=6/7\), whose modular invariant partition function is labeled as the pair of Lie algebra \((D_4, A_6)\) in the \(ADE\) classification.
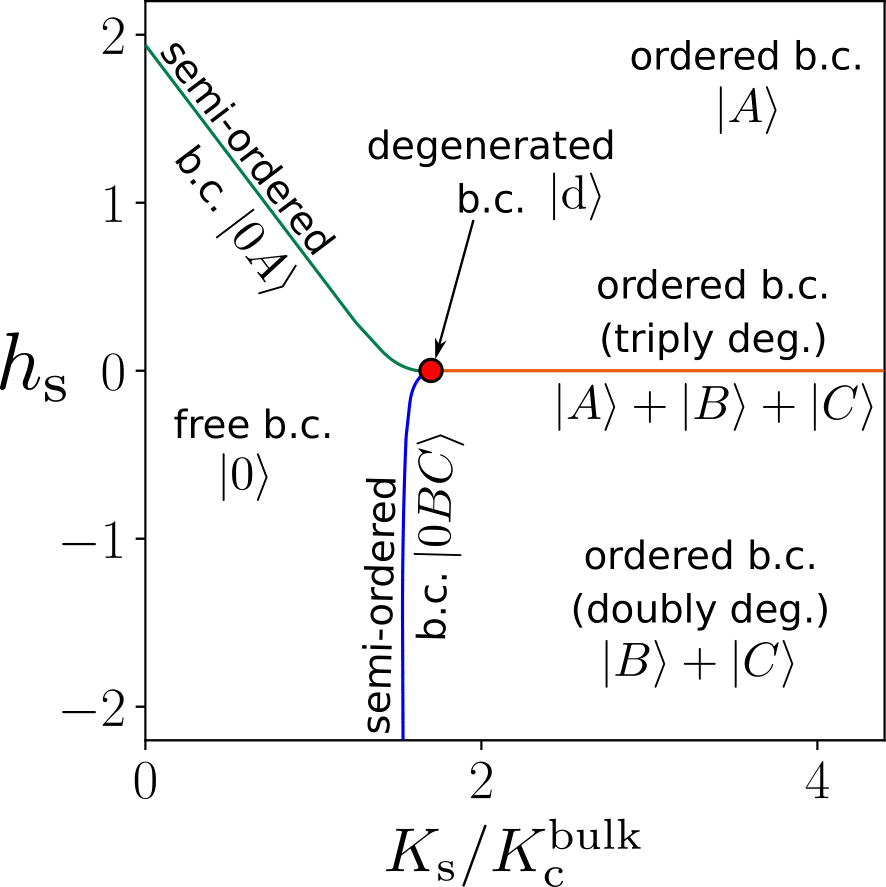
Using the complete classification of the conformal boundary states in Ref. [3], one can derive the twelve conformal boundary conditions labeled by the nodes of the Dynkin diagrams \(D_4\) and \(A_6\).
The triality of \(D_4\) implies that those can be classified into three \(Z_3\)-symmetric boundary states and nine \(Z_3\)-broken ones.
To understand the physical picture of the above twelve boundary fixed points, we simulate the 3-state dilute Potts model on lattices with the TNR technique.
The extended TNR method suited for open-boundary systems enables us to extract accurate conformal spectrum from lattice models, by which one can study the correspondence between the boundary fixed points from BCFT and the surface phases in the phase diagram of the tricritical 3-state Potts model.
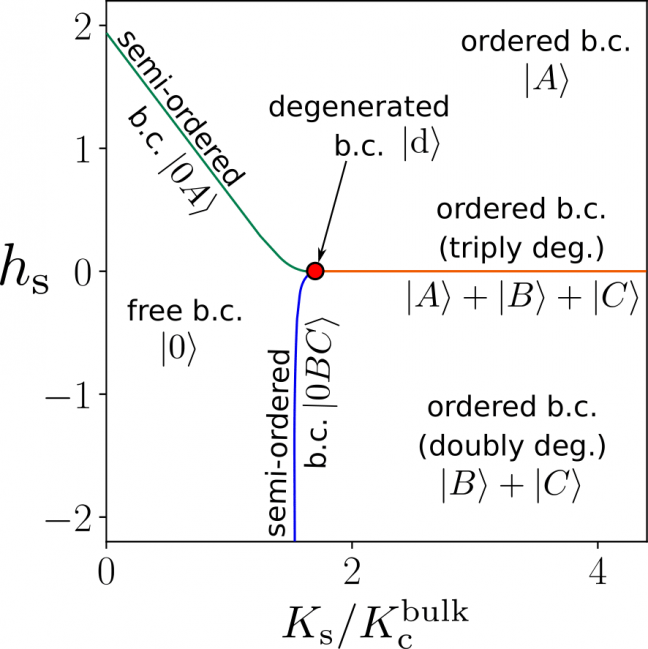
Our numerical analysis reveals that the eleven boundary fixed points among the twelve can be realized on the lattice by controlling the external field and coupling strength at the boundary.
The last unfound fixed point would be out of the physically sound region in the parameter space, and we leave it an open question to consider the realization of that boundary condition on the lattice model.
(by Shumpei Iino)
References:
[1] I. Affleck, J. Phys. A 33(37), 6473 (2000).
[2] Y. Deng and H. W. J. Blöte, Phys. Rev. E 70, 035107 (2004); Phys. Rev. E 71, 026109 (2005).
[3] R. E. Behrend, P. A. Pearce, V. B. Petkova, and J.-B. Zuber, Nucl. Phys. B 579(3), 707 (2000).
[4] G. Evenbly and G. Vidal, Phys. Rev. Lett. 115, 180405 (2015); S. Iino, S. Morita, and N. Kawashima, Phys. Rev. B 101, 155418 (2020).
[5] S. Iino, arXiv:2007.03182; J. Stat. Phys. 182, 56 (2021).