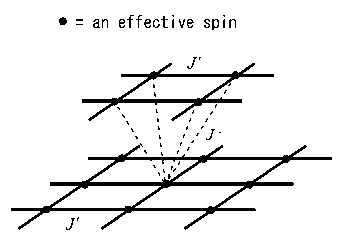
The principal effect of frustration is cancellation among competing couplings. In quasi-two-dimensional systems, when the frustration exists in inter-layer couplings, it tends to enhance murual independence of layers. At finite temperature, however, this cancellation can never be perfect so as to make the system purely two-dimensional because thermal fluctuation generates effective net interlayer couplings. Even at zero temperature, the geometric frustration fails to decouple layers completely since the zero-point fluctuations restore the inter-layer coupling as discussed by Maltseva and Coleman. As a result, the critical phenomena in any real quasi-two-dimensional system belongs to the universality class of some three dimensional theory no matter how perfectly the frustration may seem to cancel the couplings. However, we find that this is not necessarily true at quantum critical points. [1]
The first experimental evidence of this phenomenon was found by measuring critical exponents of a field induced QCP in BaCuSi2O6. [2] This is a spin dimer system whose highly symmetric crystal structure gives it unique advantages for tackling the fundamental role of dimensionality in quantum criticality. The material consists of layers stacked on top of each other forming a body-centered-cubic (BCT) lattice of dimers. By neglecting two high-energy triplet states of each dimer, the system can be represented by an S=1/2 XY model on BCT lattice. We examined the magnon excitations by using the spin-wave treatment..[1] The effective coupling between layers is proportional to the number of excited magnons, which means that the fluctuation responsible for the effective inter-layer coupling dies out as we approach zero temperature and the quantum critical point can possess purely two dimensional characteristics. Thermal or quantum fluctuations at finite temperature induce a crossover to d = 3 away from the QCP. The two-dimensional value of the exponent characterizes the phase boundary near the zero temperature, in agreement with the experiment [2].
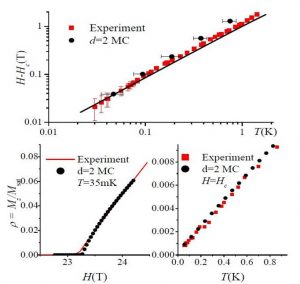
The agreement between the pure two-dimensional behavior and the real experiment is not only qualitative, but it is quantitatively good as can be seen in Fig. 2. The upper panel shows the critical field measured in the experiment on BaCuSi2O6 plotted with the phase boundary obtained by quantum Monte Carlo simulation assuming that the inter-layer coupling is zero (filled circles) . Both the results show the two-dimensional quantum criticality that is characterized by the asymptotic linear dependence. The correspondence is further confirmed by other quantities: the field-dependence of the magnetization at zero (or very low) temperature (lower left panel), and the temperature-dependence of the magnetization at critical magnetic field (lower right panel).
(by Naoki KAWASHIMA)
Reference:
[1] C. D. Batista, J. Schmalian, N. Kawashima, P. Sengupta, S. E. Sebastian, N. Harrison, M. Jaime and I. R. Fisher, Phys. Rev. Lett. 98, 257201 (2007).[2] S. E. Sebastian, N. Harrison, C. D. Batista, L. Balicas, M. Jaime, P. A. Sharma, N. Kawashima and I. R. Fisher, Nature 441, 617 (2006).